VOL.317１問全力解析　2024年度　桜蔭中学校

今回の１問全力解析は２０２４年桜蔭Ⅰ（２）です。
まずは問題を見てください。

基本テーマから見ていきましょう。

基本テーマ
１．問題文の読み取り
２．場合分け
３．全体からダメなものをひく
４．樹形図による書き出し
５．②でいかにして①を活かすか

この問題では以上のような基本テーマが潜んでいると考えられます。ひとつずつ見ていきます。

１．問題文の読み取り
７マスに黒い丸と白い丸を入れるだけです。ただし、きまりが４つあります。ここをどう解ける形に落とし込んでいくか。そこが算数的な問題文の読み取りということになります。

（あ）と（い）の条件は一緒にし、（え）は片方だけを考慮すればよいように場合分けが得策、と見抜きたいところです。

２．場合分け
（あ）と（い）のきまりで、上から２マス目が決まれば４マス目と６マス目が決まることになります。２マス目が〇か●で場合分けすれば、残りのマスは４マスですから、
最大でも２×２×２×２＝１６（通り）から、どうにでもなるという見通しが立ちます。

また、上から２マス目が〇だと（え）の条件は無視できるので、それもプラス材料ですね。

３．全体からダメなものをひく
最大でも１６通りですから書き出しでかまわないとは思いますが、実力アップのために計算で求められるようにしておきましょう。

その場合、全体からダメなものをひく（余事象の利用）が得策でしょう。
※余事象とは「ある場合以外」のできごとのことです。

４．樹形図による書き出し
実は①で場合分けをした際、片方は計算で良いと思いますがもう一方は計算よりも書き出した方が簡明だと思います。実戦的には計算で行くことを少し考えてうまくいきそうならそのまま計算し、少しでもモヤモヤしたり嫌な感じがあれば樹形図で書き出す、というのが正解確率の高いやり方だと思います。

５．②でいかにして①を活かすか
①の結果を利用して②を解くであろうことは予想がつきますが、単純に結果を利用すれば良いかというと、うまくいかない気がします。

本問の場合は①で場合分けしたその結論を活かせば良いという、いかにも本校らしいつくりになっていました。

毎年のように出題される、Ⅰの「場合の数」は本年もなかなか厄介であり、しっかり差がついたことでしょう。

以上を踏まえて問題を解いてみましょう。

（１）（あ）と（い）の条件だけを考えて上から２マス目で２通り（上から２、４、６マスの決め方は２通りだけ）に場合分けします。

ⅰ）上から２マス目が〇

残りの４マスの決め方はそれぞれ●か〇の２通りですから
２×２×２×２＝１６（通り）
（う）の条件のだめなものは
下３マスが〇

なので、上から１マス目と３マス目がそれぞれ２通りずつありますから
２×２＝４（通り）
これを全体からひいて
１６－４＝１２（通り）…①

ⅱ）上から２マス目が●

（う）と（え）の条件は上から１マス目とは無関係ですから３、５、７マス目を樹形図で書き出します。

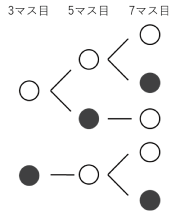
樹形図より５通り、これに対して上から１マス目は２通りずつありますから
５×２＝１０（通り）…②

①と②の和が答なので
１２＋１０＝２２（通り）…（答）

※ ⅱ）を計算で解くなら以下になります。
（う）の条件だけでだめなものは４通り…③。（え）の条件だけでだめなものは
３マス目、５マス目が●

２×２＝４（通り）…④

③と④を同時に満たすのは
３マス目、５マス目、７マス目が●

２通り。よって

１６－（４＋４－２）＝１０（通り）

（２）Ａが〇ならＤも〇、ＢとＣは●と１通りに決まります。Ａが●ならＤも●、Ｂ、Ｃは〇です。対称性を考慮すればＡが〇のときと●のときの並べ方は同じ数だけあることがわかります。
上から２マス目が〇は１２通り、上から２マス目が●は１０通りですから、積の法則を使って
１２×１２×１０×１０×２＝２８８００（通り）…（答）

いかがでしたでしょうか。

慎重に計算と書き出しの両方をすり合わせるようにすれば、かなりの確率で正解できたと思います。
Ⅰの小問に時間はかけられないとばかりに、すっ飛ばすような解き方をしてしまえば不正解でも文句は言えなかったことでしょう。
本校の場合は最高のスピードを発揮しつつも慎重さが要求される、非常に高いレベルが要求される試験だと思います。
しっかりと対策を行っていきましょう。