VOL.316１問全力解析　2024年度　筑波大学附属駒場中学校

今回の１問全力解析は２０２４年筑波大附属駒場１です。

まずは問題を見てください。

基本テーマから見ていきましょう。

基本テーマ
①問題文の読み取り
②「対応」を見抜く
③どのような制約があるか
④後ろからたどる
⑤書き出し

この問題では以上のような基本テーマが潜んでいると考えられます。ひとつずつ見ていきます。

①問題文の読み取り
Ａ、Ｂ、Ｃ、Ｄと文字が出てきますが、特に問題はないでしょう。ユークリッドの互除法に似ているようにも思いますが、今回はあまり関係ありませんでした。３７→１７→７と割る数が変化する（２０ずつ小さくなっている）ことがどのような影響を与えるかに注目するところでしょう。

②「対応」を見抜く
（１）でＢ、Ｃ、Ｄが与えられ、最小のＡも教えてくれています。「２番目に小さいものを見つけてね」というのが出題者の問いかけですから、それに応えてまずはやってみましょう。

ところが、Ｂが決まればＣも決まり、Ｄも決まるので、ヒントが多すぎます。そしてＢが決まってもＡは１つには決まらないということを問題が示しています。

商が複数考えられるのでこうなる訳です。商が「０」から「１」になるとＡがどうなるかはもうわかりますね。

※数学で習うのですがこのような対応を「多対一」と言います。

③どのような制約があるか
この問題の肝がここです。Ｂ～Ｄは「余り」なので「割る数」よりも小さくなければなりません。

Ａはそういった制限はありませんが、（２）、（３）では２０２４以下という範囲が設定されています。

④後ろからたどる
ここまで来ると、後ろからたどるのは当然と言ってよいでしょう。

その際気をつけなければならないのは（２）と（３）の違いです。

（３）は「同じ」がダメな訳です。

⑤書き出し
本質が見抜けていれば、いちいち書き出さなくても良いことがありますが、本問の場合はきちんと書き出した方が良いでしょう。

③の制約がチョコチョコと顔を出すので、書かないと危険です。

その際、いつものように樹形図がお勧めとなります。

ただし、Ａは具体的に書くのではなく個数を求めるのが良く、事前に計算しておくとスッキリ答が出ました。

以上を踏まえて問題を解いてみましょう。

（１）最小は商が「０」の時です。２番目に小さいのは商が「１」の時ですから３７増えます。
２６＋３７＝６３･･･（答）

（２）Ｂが決まるとＡの個数が決まります。
２０２４÷３７＝５４あまり２６
なので、Ｂが０～２６ならＡは５５個、２７～３３なら５４個です。

樹形図で後ろから書き出します。
その際、Ａだけは個数を書いておきます。

また、Ｂは３７未満、Ｃは１７未満、Ｄは７未満であることに注意しましょう。

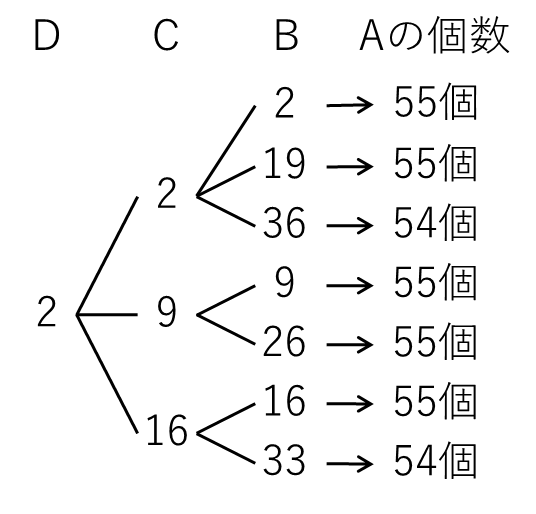
以上より求める個数は
５５×７－２＝３８５－２＝３８３（個）･･･（答）

（３）Ｂ、Ｃ、Ｄがすべて異なることに注意して、（２）と同じ要領で書き出します。

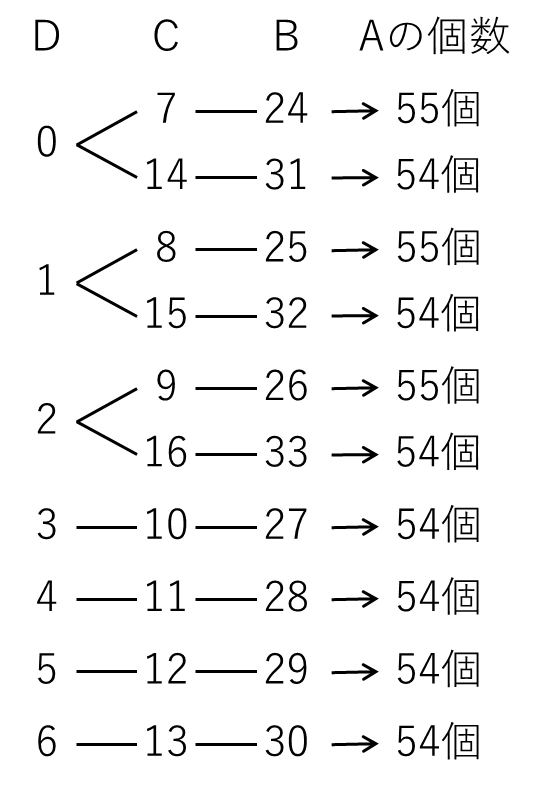
以上より求める個数は
５４×１０＋３＝５４３（個）･･･（答）

いかがでしたでしょうか。
制約がそこそこ多いので、間違えた受験生もいたと思います。
差がついた可能性もあったでしょう。
きちんとした書き出しが要求された問題だったと思います。
普段から絶対に間違えないという強い気持ちで、正解力を養いましょう。