VOL.315１問全力解析　2024年度　開成中学校

今回の１問全力解析は２０２４年開成２です。
まずは問題を見てください。

本校の【場合の数】の出題は近年同じようなテイストになっています。２０２０年３、２０２２年３、２０２３年５（１問全力解析で取り挙げ済みＶＯＬ．２７３）、そして本年２と毎度お馴染みになっていますね。

基本テーマから見ていきましょう。

基本テーマ
①問題文の読み取り
②まずはやってみる
③樹形図を使って書き出す
④アトから入れられる場所が何通りあるか
⑤誘導に乗る

この問題では以上のような基本テーマが潜んでいると考えられます。ひとつずつ見ていきます。

①問題文の読み取り
２ページに渡る長文ですが、言っていることはそんなに難しくありません。ここでは自分なりに納得することが大切でしょう。試験本番では長文だからといって焦らず、まずは落ち着くことです。

②まずはやってみる
最初は素直な気持ちで取り組みましょう。実際に机の上にカードを並べているようなつもりになれればこの問題の世界に入り込むことができます。

ただやってみるだけでなく、「４が机の上に置かれたらその後の５や６は箱の中」→「机の上は左の数が右の数より大きいような並び方」といった具合にある程度の結論まで到達できるように頑張りましょう。

③樹形図を使って書き出す
途中、「全て書き出しなさい」という設問があるのですが、このときの書き出しで便利なのが樹形図です。少しですが書く量を減らせるのと抜けやダブりが生じにくいというメリットがあるので、場合の数での書き出しの基本になっています。

本問の場合樹形図の形が解法の手掛かりになったかもしれません。

④アトから入れられる場所が何通りあるか
本問は（３）を解くのが主眼なので、そこに向かって少しずつ前進していくような作りになっています。

⑤でも取り上げますが、結局前の結果を利用するといういつものやり方がここでも得策となります。

その際、１枚カードが増えても（例えば４枚から５枚）結果が変わらない場合、増えたカードを既に並べてあるカードのすき間に入れる（先頭以外）ことを考えれば簡単に計算できます。

⑤誘導に乗る
（２）までを解いていくと、９枚で《７５４２１》になるためには、それぞれの枚数の結果に制約があることがわかります。

２枚の結果が《２１》から１枚ずつ増やしていけば９枚も恐れることはないでしょう。

その際、表を利用すると見やすくなると思います。

以上を踏まえて問題を解いてみましょう。

（１）１枚目のカードは必ず机です。以下机か箱か１つずつ調べます。
７→机
４→机
６→箱
３→机
１→机
２→箱
５→箱

以上より机に置かれたカードを順番に書くと
《７４３１》…（答）

（２）

（ア）樹形図で書き出します。

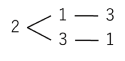
【２１３】，【２３１】…（答）

（イ）こちらも樹形図です。

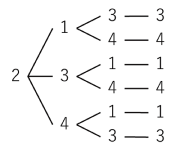
【２１３４】、【２１４３】、【２３１４】、【２３４１】、【２４１３】、【２４３１】…（答）

（ウ）①４枚で《２１》になるのは（イ）から６通りとわかります。

５枚で《２１》は、すでに４枚で《２１》になる並びの間に５を入れれば良いことになります。ただし、５が先頭にくると《５２１》になってしまうので、４枚の右側４カ所のうちのどこか５を入れるのが何通りあるかということになります。

６×４＝２４（通り）…（答）

②上で検討したように先頭に５がくるケースですから

（答）６通り

（エ）すぐ上の②で求めた５枚の並びの右横に６を入れればよいので

６×５＝３０（通り）…（答）

（３）上の（ウ）（エ）でやったようなことを表にまとめます。

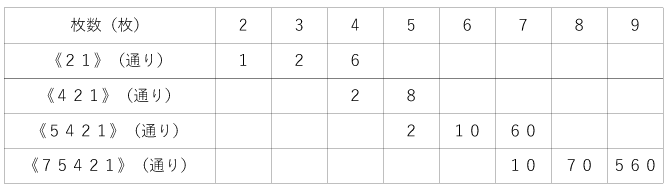
※ 表を横に見た時、『１つ右はその数と一番上の数字をかけたものになっている』。
縦に見た時、『１つ上はその数と１つ左の一番上の数字をかけたものになっている』。

表より

（答）５６０通り

いかがでしたでしょうか。

本問の場合は１つ前の結果に対して次のカードを間に入れるという発想でうまくいきました。その際、結果として考えられるのは２通りだけで、そのうちのひとつは入れ方が１通りしかないというのがポイントでした。

以上のようなことに気付けば、完答も可能だったでしょう。

誘導を無視した場合は（３）の正解はほぼノーチャンスだったと思います。

今年も本校の「正解してね」という温かさに触れることができ、とても嬉しく思います。