VOL.313１問全力解析　2024年度　浦和明の星中学校

今回の１問全力投球は浦和明の星女子２０２４年 第一回【４】です。
まずは問題を見てください。

解くための基本テーマは以下になります。

Ⅰ周回運動の基本知識
Ⅱ比を使う
Ⅲ対称性を考慮する
Ⅳシャドゥの設定
Ⅴグラフを描く

以上が考えられます。Ⅰ〜Ⅴそれぞれについて少しコメントします。

Ⅰ池の周りを反対方向に周回する場合、何回も出会うことになります。速さの比がＡ：Ｂの場合、出会う地点は（Ａ＋Ｂ）カ所になり、初めてスタート地点で出会うまでにＡの方がＡ周、Ｂの方がＢ周します。（ＡとＢは共に整数かつ互いに素）

Ⅱ旅人算で解こうとすると、距離と速さを適当な数値で設定する必要があるので、得策ではないかもしれません。比を使って解けばスンナリいきそうだという見通しを立てたいところです。

Ⅲ（２）と（３）は両方とも親切にも２回と教えてくれています。対称性を考えれば、行きと帰りで２回という結論にたどり着くでしょう。同時にＡに着くということは逆にたどればスタート直後と線対称の動きになります。

Ⅳ（２）（３）は共にシャドゥを設定すると追い越しになります。スタート地点を変えることで両方とも解決します。

Ⅴシャドゥを設定して追い越しとなると「旅人算」で解くのが一般的でしょう。ここでは別の解法として「グラフ」を推奨したいと思います。答が２つということもすんなり解ります。ということは、「２つ」というヒントが無ければ「グラフ」が最善かもしれません。

以上を踏まえ問題を解いてみましょう。

〈解説〉

（１）速さの比が４：１なので同じ時間で進む道のりも４：１です。
３６０度を４：１に分けた１の方が答です。

３６０✕  １  ４＋１  ＝７２（度）…ア（答）

２点が出会う場所は
４＋１＝５（カ所）
で、その間Ｑは１周するので

（答）５回目　…イ

（２）
〈図１〉

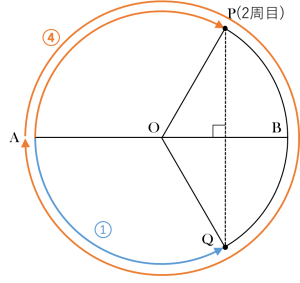
〈図１〉から明らかなように④と①の差である④－①＝③が１８０°にあたるので

１８０×  １  ３  ＝６０（度）…（答）

これが行きだとすると帰りは

３６０－６０＝３００（度）…（答）

（３）
〈図２〉

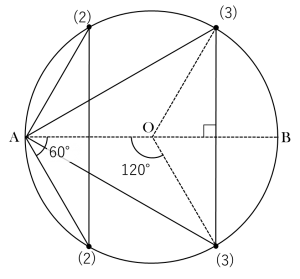
Ｐの１周目では問題文の条件のようにはならないので２周目を考えます。〈図２〉
Ｐが１周分多く進んでいるので差は３６０°です。よって

３６０×  １  ３  ＝１２０（度）…（答）
帰りは
３６０－１２０＝２４０（度）…（答）

（４）
〈図３〉

〈図３〉より、内部底辺が３倍で高さが同じですから
（答）１：３

〈別解〉

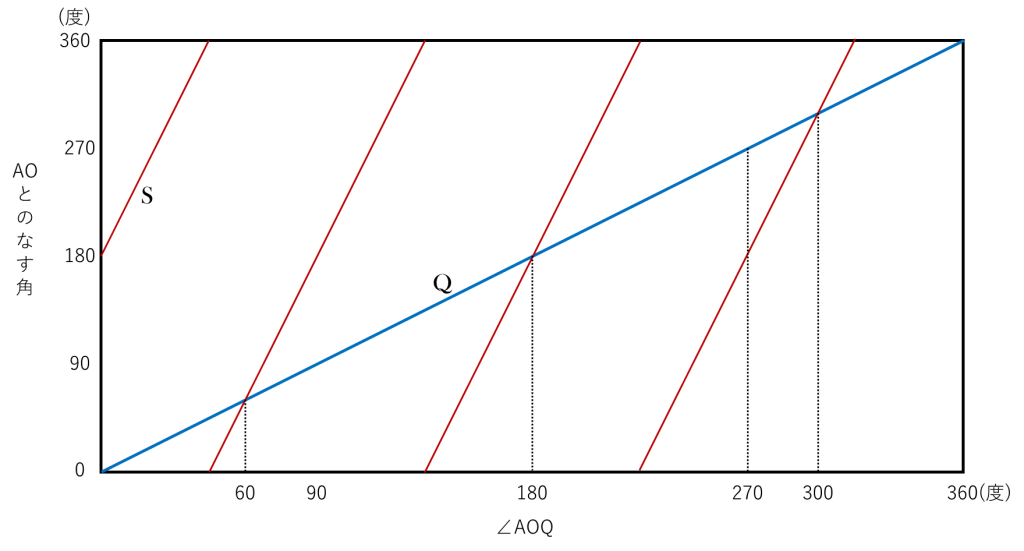
（２）グラフを描きます。Ｐと逆回りでスタート地点がＢのＳを設定します。横軸が∠ＡＯＱ、縦軸がＡＯとのなす角でＱとＳについて描きます。
〈グラフ１〉２本の線が交わったところが答ですが、１８０°のところはＡＢと重なるので不可です。

〈グラフ１〉

グラフより
（答）６０度、３００度

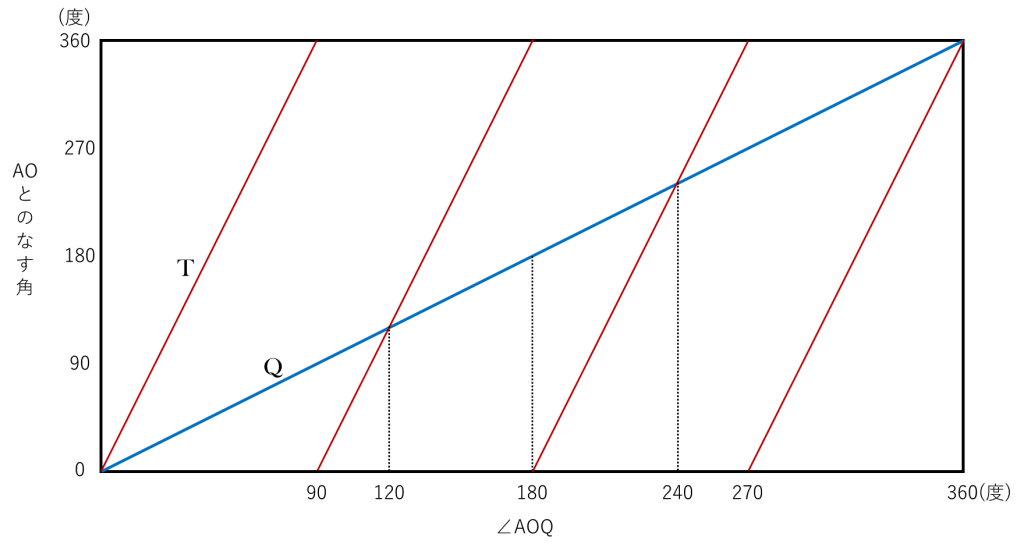
（５）Ｐと逆回りのＴを設定します。〈グラフ２〉

〈グラフ２〉

グラフより
（答）１２０度、２４０度

いかがでしたでしょうか。

様々なテクニックを使うことができた差がつく問題だったと思います。

新６年生はこれからの１年間で役立つ知識をしっかりと身に着け、ライバルに差をつけましょう！