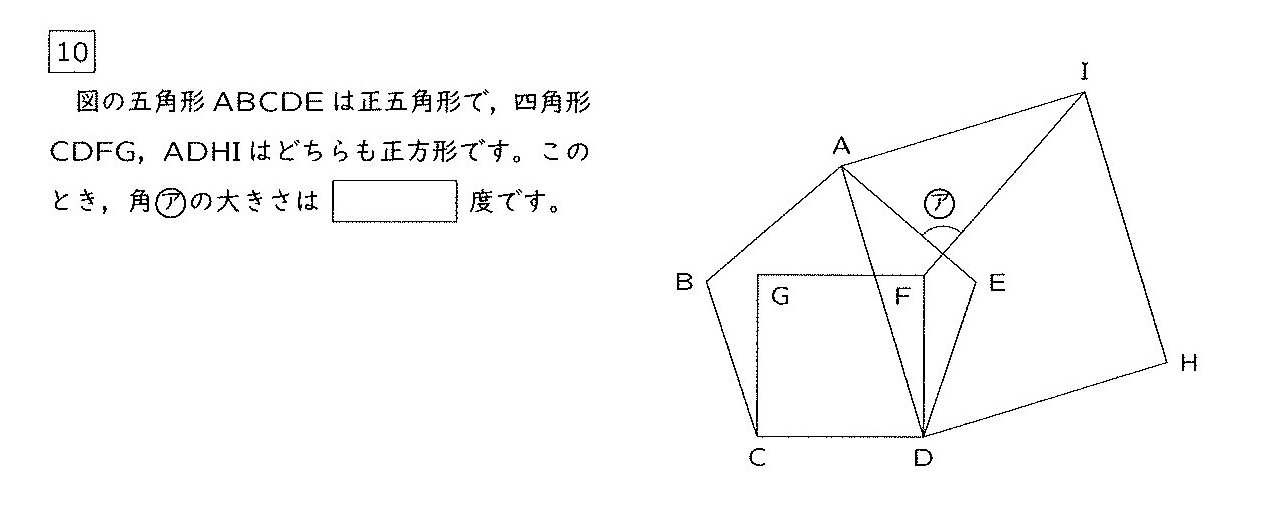
VOL.3121問全力解析 2024年度 灘中学校 1日目
今年度最初の1問全力解析は2024年灘1日目10です。
まずは問題を見てください。
基本テーマ
(1)正方形2つで思い浮かぶもの
(2)合同の発見→なければ作る
(3)二等辺三角形の発見
(4)正五角形についての知識
(5)どこを知りたいかを明確にする
まず(1)はよくある問題を思い出して欲しいということです。大小の正方形が出てくる〈図1〉のような問題ですね。ここでは△AED≡△CGDがポイントです。
〈図1〉
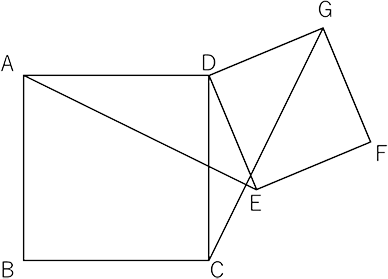
正方形が1つの頂点を共有して2個出てくるような場合は合同な三角形があるぞ、という見通しが大切です。
そうすると、(2)はほぼ必然となります。ところが本問の場合は肝心な三角形がありません。そこが厳しいところなのですが、なければ作るという積極性が正解を手繰り寄せます。
〈図2〉のような補助線を引けば当初の目標は達成となります。
〈図2〉
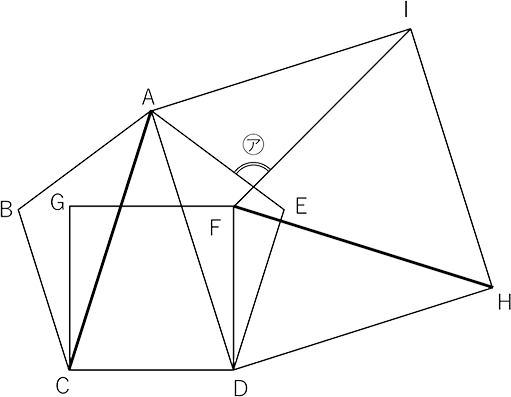
そして、次の(3)にスムーズに繋がれば正解したも同然です。
今週の1題だとVOL.230のような問題に触れていればこの二等辺三角形の発見は容易でしょう。
ここまでで正解は可能ですが、以下2つは主に効率化に寄与するものです。(4)は、正五角形の角度について頭に入れておくと良いものです。
1つの内角は108°ですが、対角線5本を引いた場合も36°、72°、108°しか出てこないことを知っておくと便利です。本問の場合、2箇所の36°を「知っている」で片づけられればスマートに解けました。
最後の(5)は考え方の方向についてです。
∠IAEが求まることから、知りたいのは∠AIFということになります。
そこから逆にたどると∠FIH ⇒∠FHI ⇒∠FHD ⇒∠CADとなり、「解けた~」となります。分かっているもの、すぐに分かりそうなもの、分からないもの(それが分かれば答がでるもの)の区別がつけられるようにしましょう。
以上を踏まえて問題を解いてみます。
〈解説〉
〈図2〉を使って説明します。
△ACD≡△HFD (2辺とその間の角がそれぞれ等しい)
なので
AC=AD=HD=HF=HI
となります。よって△FHIは二等辺三角形です。
∠FHI=90°-∠FHD=90°-36°=54°
∠FIH=(180°-54°)÷2=63°
∠AIF=90°-63°=27°
また
∠IAE=90°-36°=54°
よって求める答
㋐=180°-(54°+27°)=99° …(答)
いかがでしたでしょうか。何の経験もなければ解くのに苦労したかもしれません。しかし、本校の受験生ならばお馴染みの問題を少し捻った程度だったでしょう。
図形問題を解く際の考え方が詰まった角度の良問だと思います。
今後の学習では、なるべくこのような良問に多く触れ、センスを磨いておくことが得策と言えるでしょう。
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の1題円周角の定理と図形の角度
難易度★★★☆☆
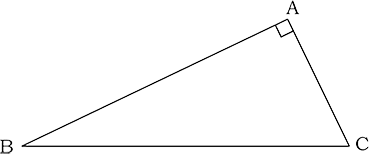
〈図1〉のような∠A=90°、∠B=30°の直角三角形があります。△ABCに外接する円を描いたものが〈図2〉で、円の中心がOです。
〈図3〉は、∠BAD=40°、∠DAE=30°となるように円周上に2点D、Eをとり、AEとBCの交点をFとしたものです。
これについて、以下の問に答えなさい。
〈図1〉
〈図2〉
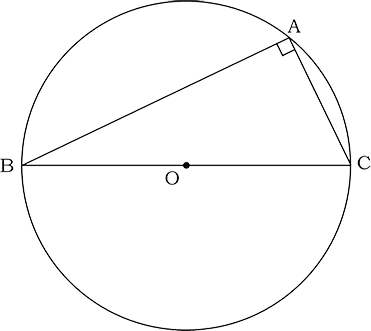
〈図3〉

(1)∠DOEは何度ですか。
(2)∠ADFは何度ですか。
解答が表示されます