VOL.39志望校対策(12) 「豊島岡女子学園」
志望校対策の最後は豊島岡女子学園です。
本校の算数は比較的オーソドックスだと思います。
大問1、大問2が計算を含む小問集合で、その後ろの大問が4題程度です。
ほぼ難易度順に並んでいて、後半は「数論」「速さ」「図形」が頻出でやや骨があるという傾向が見て取れます。
合格者平均点は7~8割と高めです。
最近の受験生は見たことがあるような問題は確実に正解するので、妥当な結果でしょう。
解答欄には答のみを書く方式で部分点はありません。ミスの許されない厳しい試験です。
それでは対策を考えていきましょう。
本校の受験生ならば1、2番の小問は基本問題の範疇でしょう。
ここは満点(8問40点)を狙いたいところです。
前半で40点をキープし、残りの半分(10問中5問)を取れれば勝負になります。
よって、対策は2段構えにしておくのが良いでしょう。
① 基本的な問題をスピーディーかつ正確に解けるようにする
② 差がつきそうな問題で正解する側にまわる
①については、計算を含め幅広い分野で苦手がないように十分に練習しておく必要があります。
ただし、基本問題とはいっても、それはあくまで本校の受験生のレベルでのことです。
一般的な受験生にとっては少しひねってあったり、高級な考え方が必要な問題ということになりますので、注意が必要です。
大抵は「知っている」で片付けることができるので、普段の学習で「深さ」を意識しておくと良いでしょう。
「知識」とする場合は忘れてしまうと困るので、繰り返し学習し、定着をはかってください。
また、後半に時間を残す意味でも、前半はスピーディーに解きたいところです。
急いで解くのではなく、「ゆったりと解くのに結果的にはやい」という境地を目指しましょう。
このあたりの考え方はVOL.34の「女子学院」のところを参考にしていただければと思います。
当たり前ですが、②が入試の合否を分けるポイントになります。
まずは苦手分野を作らないことが肝心です。
頻出である「数論」「速さ」「図形」で算数の主要テーマはほぼカバーされていますから、バランスの良い学習が要求されます。
それらの分野全てで「やや難」レベルまで解けるような準備をしておかなければなりません。
「やや難」レベルまで解けるようにするにはどうすれば良いかを「速さ」を例に説明したいと思います。
「速さ」をさらに分類(「流水算」等別に名前がついているものは除く)すると、「速さの3公式」「速さと比」「往復」「周回」等にわけられます。
それぞれ基本となる問題があり、その範囲の中で難易度が高い問題もあります。
分野を跨がない問題に関しては一番難しいものまでやっておくのが得策です。
例えば「周回」を学ぶならば、基本的な問題集の「周回」のところは一番難しいところまで全部やるということです。
そして、その結論はある程度「知識」とします。
これは①の対策でもあります。具体例をいくつか挙げます。]
- 池の周りをA、Bの2人が同じ地点から反対方向に同時にスタート。速さの比が3:2ならば初めてスタート地点で出会うまでにAは3周、Bは2周する。
- 池の周りをA、Bの2人が同じ地点から同時にスタート。反対方向だと1分で出会い、同じ方向だと3分でAがBに追いつくとき、AとBの速さの比は2:1。
- 池の周りをAは3分で1周、Bは2分で1周する。2人が池の反対側から逆方向にスタートすると30分の間に2人は25回出会う。
これらを、なぜそうなるかを含め、完全に頭に入れておくことが望ましいです。
そうなってくると難しいのは教材選びです。
教材によっては、難しい問題はいろいろな分野が入ってきているものもあります。
そうなると知識にはしにくいので効果が弱まります。
シンプルでありながらある程度深い教材を使うのが良いのです。
この教材の選定は専門家に任せるのが良いでしょう。
中にはオリジナルの教材を用意してくれる場合もあります。
これからは時間がありませんから余計なことはしてはいけません。
合格に直結するものだけを厳選する必要があるでしょう。
「知識」を充実させたあとはそれを使う練習です。
それには「過去問演習」が効果的です。
計画を立てて、最低でも10年はやりましょう。
本校の過去問はもう終わったという受験生は他校のもので代用すると良いでしょう。
その場合1年分まるまるやるのも良いですが、分野ごとに似たような問題をピックアップしてやるのも効果的です。
指導者に優先度を判断してもらいながら選んでもらってください。
このように実際の入試問題を基本的な「知識」を使って解く練習をすることにより、やや難しい問題も正解できる可能性が高まるでしょう。
いたずらに難しい問題に取り組むよりも、このようにして基本から積み上げた方が効率が良いのです。
まとめます。
- 前半はスピードと正確性が大切。40点満点を目指す。
- 後半はそれなりに骨がある。頻出分野に苦手がないようにし、やや難レベルまでは解けるように準備する。
- 後半は半分正解でなんとかなる可能性が高いが、できるだけ多く正解するという気持ちは忘れない。
- 普段の学習は「基本+α」までを完全に自分のものにしておく。結論はある程度「知識」とし、過去問等を利用し使いこなせるように練習する。
- 概ね難易度順に並んでいるが、「危ない」と感じたら一旦後回しにすること。「立体」図形の難問は場合によっては解かなくてもよい。
本校の場合はいかに失敗を回避するかということが大切です。
ミスをすると最低でも5点消えてなくなります。2つのミスは取り返すのが相当に困難でしょう。
また、難問に時間を使いすぎることも避けなければなりません。
解答順が大切ですし、試験中に作戦を練る必要もあるかもしれません。
これらは全て経験が大切になります。残りの期間はわずかですが、模試や実際の入試を利用して最終調整を行ってください。
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の練習問題豊島岡女子学園
難易度★★★★☆
〈図1〉のように、1辺が24cmの立方体ABCD-EFGHがあります。
この立方体を3つの平面P、Q、Rで切ることを考えます。
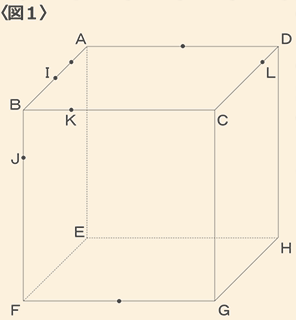
平面Pは、辺AB、辺AD、辺FGそれぞれの中点を通る平面です。
また、辺ABの中点をIとします。
平面Qは、平面Pと平行で、辺AB上の頂点Aから6cmのところを通る平面です。平面Rは、〈図1〉の3点J、K、Lを通る平面で、BJ=BK=DL=6cmです。
(1)
平面Pと平面Rが正方形ABFE上で交わる点をMとすると、IMの長さは、正方形ABFEの対角線の長さの何倍ですか。
(2)
平面P、Q、Rで立方体を切断したとき、平面Pと平面Qにはさまれた立体は平面Rで2つに分けられますが、そのうち、面EFGHを含む立体の体積を求めてください。
解答が表示されます













