VOL.293１問全力解析　麻布中学校

今回の１問全力解析は２０２３年麻布５です。
まずは問題を見てください。

この問題では以上のような基本テーマが潜んでいると考えられます。
ひとつずつ見ていきます。

①やってみる
似たような問題をやったことはあるかもしれませんが、全く同じ設定は初めてだったと思います。
初見の問題に対しては「まずやってみる」という姿勢が大切です。
この問題の場合は「他のブロックと接する面の数が３つ以下のブロック」がどのようなブロックかをつかめるまでやってみる必要があると思います。

②立体を平面的に捉える
立体の問題で絶えずつきまとうのは、問題が平面で提示される上、解く際も紙の上に描かなければいけないという問題です。

平面上に立体っぽく描く手法が見取り図ですが、描く手間の関係で極力避けたいというのが本音です。

③具体的にはどうするか
見取り図がダメならどうするのか。
ここでも輪切り方式が有力でしょう。
やはり、立方体の積木は輪切り方式が最有力と考えて良いと思います。
（２）に「５×７×７」があるので「７×７」の５階建に少し憂鬱になったかもしれませんが…

④対称性の利用
作図の時特にそうなのですが、同じものを２つ描く必要はありません。
左右対称なら右だけ描けば良いのです。
立体の場合対称性を利用すれば作業量を大幅に減らすことが可能です。
具体的にどうするかは解説で披露させていただきます。

⑤それであっているかの確認
上の手法で答を求めるとあまりにもあっさりと答が出てしまいます。
話が上手すぎると不安になることもあるでしょう。
この問題の場合はど真ん中のブロックに最短距離で到達するルートのような感覚に近いので、その線に沿って確認すれば良いと思います。
全体を押さえながら答を求め、確かめる時は１点突破のイメージです。
以上を踏まえて問題を解いてみましょう。

〈解説〉
（１）
取り除く順番（１～３）を見取り図に書き込むと〈図１〉のようになります。
〈図１〉

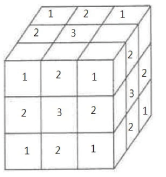
３まで取り除くと残るは真ん中の１個なので
３＋１＝４（回）…（答）

（２）
まず２４５を素因数分解します。
２４５＝５×７×７
よって２４５を３数の積で表す表し方は
①１×１×２４５
②１×５×４９
③１×７×３５
④５×７×７
の４通りあります。
①は両端は１面だけ、それ以外は２面しか接していないので操作は１回です。
②③１階建の場合、まず周の１列が取り除かれます。その後も周１列が取り除かれ、①のような１本になると１回の操作で終了です。
②１×５×４９→１×３×４７→１×１×４５→０…３回
③１×７×３５→１×５×３３→１×３×３１→１×１×２９→０…４回
④ここが本問の主眼です。
パッとはわからないので輪切り方式で描くことにします。
７×７の５階建なのですが１階と５階、２階と４階は同じなので、３階分だけ描きます。

また、正方形は線対称かつ点対称なので、ど真ん中を左上に持ってきた４×４だけ描くことにします。
☆は各階の真ん中、★はど真ん中で最後に取り除かれるブロックです。
１階・５階☆は７

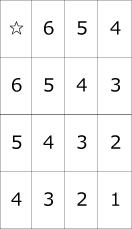
２階・４階☆は８

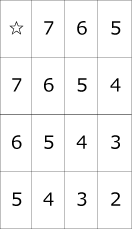
３階★は９

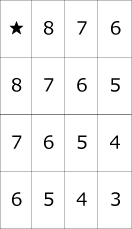
以上の検討により９回。

（答）
（２４５ｃｍ，１ｃｍ，１ｃｍ，１回）
（４９ｃｍ，５ｃｍ，１ｃｍ，３回）
（３５ｃｍ，７ｃｍ，１ｃｍ，４回）
（７ｃｍ，７ｃｍ，５ｃｍ，９回）

※確かめ５階の７×７の中央を取り除くには７回必要。
そこから奥３個目がど真ん中なのでど真ん中を取り除くのに７＋２＝９の９回かかる。

いかがでしたでしょうか。
意外とあっさりと答が出ましたね。
確かめまでしっかりやればかなりの自信度で試験を終えることができたと思います。

立体の問題でも丁寧に取り組めば十分に得点源になることが実感できたのではないでしょうか。
立体図形が得意になるとライバルに差をつけ易くなりますよ。