VOL.292１問全力解析　桜蔭中学校

今回の１問全力解析は２０２３年桜蔭Ⅰ(３)です。
まずは問題を見てください。

この問題では以上のような基本テーマが潜んでいると考えられます。ひとつずつ見ていきます。

①グラフの読み取り
グループⅠの帯グラフはそのままでも使えますが、「線分図」か「表」に書き直すと分かりやすくなると思います。
線分図に書き直す場合は左の２つを入れ替えるとすんなり描けます。

②集合の基本
ＡとＢの場合は
・両方〇
・Ａのみ〇
・Ｂのみ〇
・両方×
の４パターンが考えられ、ＢとＣについても同様です。

これがＡとＢとＣになると
・３つとも〇
・ＡとＢ〇
・ＢとＣ〇
・ＣとＡ〇
・Ａのみ〇
・Ｂのみ〇
・Ｃのみ〇
・３つとも×
の８パターンに増えます。このことは最低限押さえておきましょう。
また、３つとも〇となるためにはその前提としてＡとＢが〇である必要があることを確認しておいてください。

③情報を書き留める
問題中にあるグラフに数字を書き込んでも良いですが、別のところに数字を書き留めるのも有力です。今回は表にまとめてみます。
〈表１〉ＡとＢ

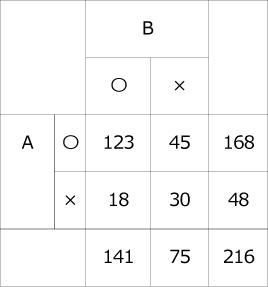
〈表２〉ＢとＣ

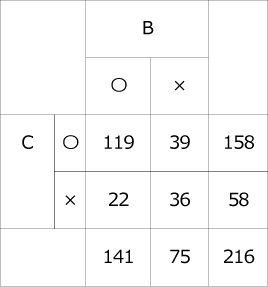
帯グラフから上の２つの表をおこすのは容易だったと思います。

④書き留めておいたものに情報を加える
グループⅠの情報にグループⅡの情報を加えます。
その際、全体の５２．８％と２．８％はあらかじめ計算しておきます。
２１６×  ５２．８  １００  ≒１１４（人）
２１６×  ２．８  １００  ≒６（人）

また、２つの時に４パターンだあったものが３つになると倍の８パターンになっています。
これはＢとＣだけだと４パターンですがそれぞれのマスにつきＡが〇か×かの２パターンあり４×２＝８の８パターンになると考えることができます。

ＢとＣのところにＡが〇か×かの情報を書き加えます。
〈表２〉中ほどの４マスについてそれぞれのマスを２つに分けて８マスにし、それぞれＡが〇は左、×が右にくるように数字を書き入れます。

〈表３〉

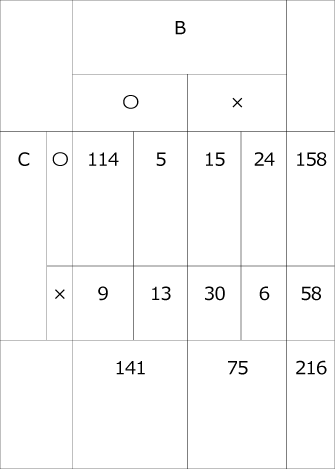
この表が完成すれば正解はすぐそこでしょう。

⑤計算・確かめ
グループⅡの円グラフが百分率なのでその計算をしなければなりません。

結局割り算の筆算は避けられないでしょう。
分数として見た時の分母は２１６で約分ができそうなのですが、あいにく分子が２９と６７で共に素数です。
そのあたりまで狙って問題を作っていると思われるので、本校は油断がなりません。

確かめとして、人数の合計が２１６人となることと、割合の合計が１００％になることは求めておきましょう。

以上を踏まえて問題を解いてみましょう。

〈解説〉
〈表１〉〈表２〉より
（答）エ１６８　オ１４１　カ１５８

ＡとＢ両方〇の合計が１２３人のうち、Ｂ〇Ｃ×を除いた人数が３つとも〇です。

Ｂ〇Ｃ×の最大値は２２なので

１２３－２２＝１０１…キ（答）
〈表４〉

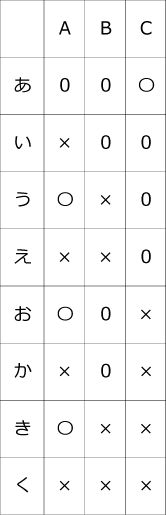
〈表３〉を完成させる手順を説明します。あ～くが何を示すかをまとめたのが〈表５〉です。

〈表５〉

上の④の計算結果より
あ…１１４く…６
以下芋づる式に数字が求まります。
い…１１９－１１４＝５
お…１２３－１１４＝９
か…２２－９＝１３
き…３６－６＝３０
う…４５－３０＝１５
え…３９－１５＝２４

２つ〇…いうお５＋１５＋９＝２９
 ２９  ２１６  ×１００≒１３．４（％）…ク（答）

１つ〇…えかき２４＋１３＋３０＝６７
 ６７  ２１６  ×１００≒３１．０（％）…ケ（答）

いかがでしたでしょうか。

何となく煩わしいのは本校ではいつものことですが、数字の煩雑さというよりも集合そのものの捉えにくさから来ているように感じました。
こういった問題で頭を鍛えることは、算数の実力アップに大いに繋がると思います。