VOL.2881問全力解析 2023栄光学園
今回の1問全力解析は2023年栄光学園2.です。
まずは問題を見てください。
基本テーマ
①立方体の積木の切断
②平面で捉える
③輪切り方式
④前の答の利用
⑤確かめ
この問題では以上のような基本テーマが潜んでいると考えられます。
ひとつずつ見ていきます。
①立方体の積木の切断
立方体の積木と立体の切断という2つのテーマの融合です。
基本的に2つ以上のテーマが含まれる問題は難しくなりますから、それなりの対応をしなければ苦戦は免れないでしょう。
以下は必要と思われる技術になります。
②平面で捉える
立体の問題は平面で捉えなければ対応が難しいと思います。
平面で捉えるためには、方向を定めなければなりません。
この問題の場合は最終的には3つの平面で切断することになるのですが、最初に切った平面が線に見える方向から見るのが良いと思います。
③輪切り方式
輪切り方式は立方体の積木では特に有効です。
この問題の場合は手前、真ん中、奥の3層に分けて考えるのが得策でしょう。
それぞれの層を作図するのか、作図の量を減らすため1つの層を流用するのかは受験生自身の習熟度によります。
解説では作図は1つだけにして、後はイメージで解決することにします。
④前の答の利用
切断面が1つ増えるごとに、切断されて細かくなる立体も増えます。
よって、新たな面で切断されるたびに、どれだけ立体が増えるかを考えれば良いわけです。
まずは、新たな切断により増える数を考えることにします。
⑤確かめ
前に比べてどれだけ増えるかを考えて答を出したので、確かめは素の状態から数えるようにしましょう。
(3)(イ)の確かめで数値が一致すれば全問正解と見て差支えないでしょう。
以上を踏まえて問題を解いてみましょう。
(1)まずはA、B、Gを通る平面で切った状態を、AとB、GとHが重なる方向から見た平面図を描きます。
〈図1〉
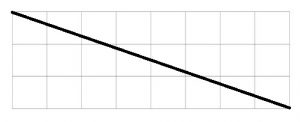
(ア)対角線によって切られた正方形の数は10個です。
切られていないのは
3×8-10=14(個)
です。これが3層になっているので
14×3=42(個)…(答)
(イ)切られると体積は1cm3未満になります。
1回の切断で立方体は2個に分かれますから
10×2×3=60(個)…(答)
(2)〈図1〉を上から1段目、2段目、3段目と呼ぶことにします。
また、手前、真ん中、奥の3層になっている、という見方をします。
A、D、Fを通る平面で切る場合切られるのは
1段目→奥
2段目→真ん中
3段目→手前
(ア)新たに切られることが無いのは
1段目→手前・真ん中
2段目→手前・奥
3段目→真ん中・奥
よって切られていないのは
(5+4+5)×2=28(個)…(答)
(イ)切られていなかった立方体が切られると1cm3未満の立体は2個増えます。
既に切られている立方体は2個だったものが4個になるので、こちらも2個増えます。
よって
60+(5+4+5)×2+(3+4+3)×2=108(個)…(答)
(3)B、C、Eを通る平面で切る場合切られるのは
1段目→手前
2段目→真ん中
3段目→奥
(ア)新たに切られることが無いのは
1段目→真ん中
2段目→手前・奥
3段目→真ん中
よって切られていないのは
5+4×2+5=18(個)…(答)
(イ)
◎1・3段目
切られていなかった立方体が切られると1cm3未満の立体は2個増えます。
既に切られている立方体は2個だったものが4個になるので、こちらも2個増えます。
よって増える立体の数は
8×2×2=32(個)
◎2段目
2段目は既に(2)で切られているところ、さらに切られることになるので
・1面で切られていたものが2面で切られる→2個増える…4個有り
・2面で切られていたものが3面で切られる→4個から7個、3個増える…4個有り
よって増える立体の数は
2×4+3×4=20(個)
以上より求める答は
108+32+20=160(個)…(答)
※確かめ
2個→5×4+3×2+4×2=34(個)
4個→3×2×2+4=16(個)
7個→4個
2×34+4×16+7×4=160(個)
※3面で切られると7個に分かれることについて
平面を3本の線でいくつの領域にわけるのかというのと同じです。
見取り図を描いて確かめるのも良いでしょう。
いかがでしたでしょうか。
今回は〈図1〉を最大限に活かすことを考えました。
1つの平面図を軸に立体を攻略する様子を参考にしてもらえればと思います。
やはり立体は平面的に捉えることが必須となりますね。
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の1題立体図形
難易度★★☆☆☆
〈図1〉は白い小立方体63個と青い小立方体62個が交互になるように組み合わせて大きな立方体を作ったものです。
〈図1〉
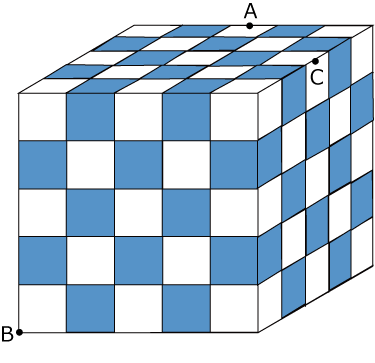
今、この立方体を3点ABCを通る平面で切断する事を考えます。
ただし、AとCは辺の中点、Bは頂点です。
(1)切断される白い小立方体と青い小立方体はそれぞれ何個ですか。
(2)切断面の白い部分と青い部分の面積比を求めて下さい。
解答が表示されます