VOL.285１問全力解析　2023渋谷教育学園幕張中学校

今回の１問全力解析は２０２３年渋谷教育学園幕張４です。
まずは問題を見てください。

この問題では以上のような基本テーマが潜んでいると考えられます。
ひとつずつ見ていきます。

①特別な二等辺三角形
中学受験における特別な二等辺三角形といえば以下が思い浮かびます。
（Ａ）正三角形
（Ｂ）直角二等辺三角形
（Ｃ）３０° ７５° ７５°の二等辺三角形
（Ｄ） √２ √５ √５ の二等辺三角形
本問は（Ｃ）の二等辺三角形がテーマになっています。
それぞれにつき、しっかりと理解を深めておく必要があります。

②角度の認識
まずは（Ｃ）の二等辺三角形の角度について、事前に知っておくべきことを挙げます。
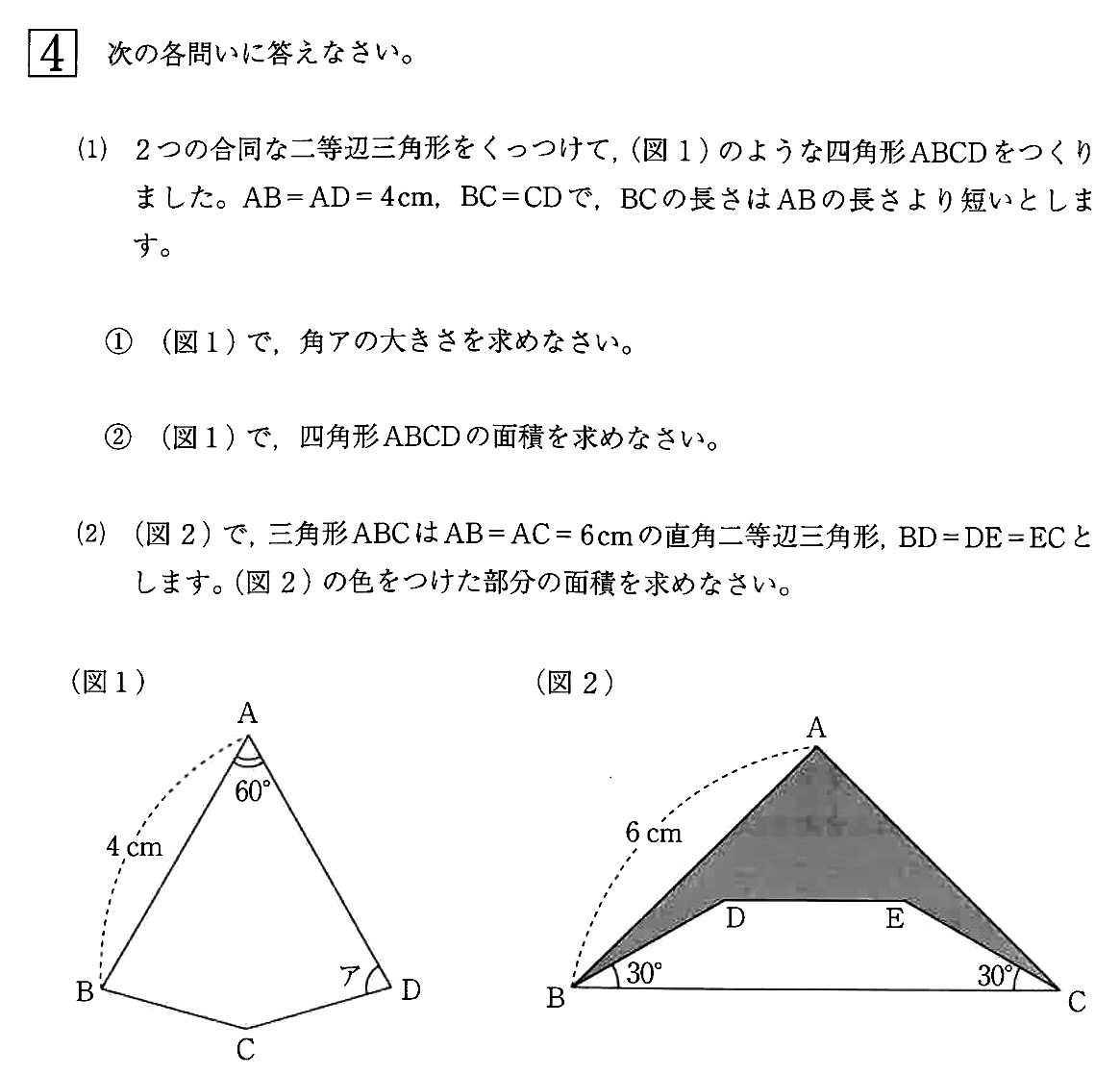
〈図１〉

正方形ＡＢＣＤの中に正三角形ＥＢＣがはめ込まれた様子です。
正方形と正三角形の性質、正方形と正三角形の１辺の長さが等しいことから図中の色々な角度を求めることができます。
〈図１〉中の角度が全部頭に入っていれば十分です。

③面積の認識
面積の認識は角度の認識よりも単純です。
正方形ＡＢＣＤ：二等辺三角形ＡＢＥ＝４：１
これだけしっかりと頭に入れておきましょう。

④よくある応用問題
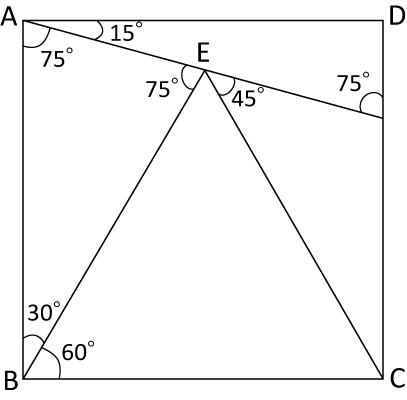
〈図２〉

〈図２〉で∠ＦＢＣ＝３０°，ＢＣ＝ＢＦです。
出題の仕方は色々あると思いますが、〈図２〉の四角形ＡＣＦＥの面積は三角形ＡＢＥの面積と等しいというのが結論です。
本問の場合は五角形ＡＥＦＣＤの面積をきいていますが、それも三角形ＡＢＥの面積に等しいですね。

（Ａ）正方形ＡＢＣＤの面積を４とおけば

（Ｂ）直角二等辺三角形ＡＢＣの面積は２

（Ｃ）二等辺三角形ＡＢＥの面積は１

（Ｄ）四角形ＡＣＦＥの面積は二等辺三角形３つから直角二等辺三角形を引いたものなので
１×３－２＝１

（Ｅ）五角形ＡＥＦＣＤの面積は直角二等辺三角形から四角形ＡＣＦＥを引いたものなので
２－１＝１

⑤どこまで記憶しておくべきなのか
本問を何の予備知識もなく１から解こうとした場合、かなりのエネルギーが必要となったでしょう。
ある程度まで知識でカバーするのは入試に制限時間があることから仕方のないことだと思います。
上の③までは頭に入れておくのは当然でしょうが、④の（Ｄ）か（Ｅ）まで頭に入っていれば本問は点を取らせてくれる問題となったことでしょう。
特に（Ｄ）は頻出なので結論を知っておくことをおすすめします。
それに対して（Ｅ）は（Ｄ）から容易に導けるので、重要度は低いと思います。
単純な記憶の量はなるべく減らした方が良いです。

以上を踏まえて問題を解いてみましょう。

〈解説〉
（１）
①三角形ＡＣＤは二等辺三角形なので
（１８０－６０÷２）÷２＝７５（度）…（答）
②１辺が４ｃｍの正方形の面積の４分の１が２個なので
４×４÷４×２＝８（ｃｍ^２）…（答）

（２）
１辺が６ｃｍの正方形の面積の４分の１に等しいので
６×６÷４＝９（ｃｍ^２）…（答）
いかがでしたでしょうか。

知っていれば即答に近かったと思います。
１から考えてきちんと正解した受験生は立派なのですが、結果に結びついたかどうかは疑問です。

本校の場合は本問のような「知っている」で片づけることが可能な問題が頻出なので、「知識の充実」をしっかりとおこない、そのうえで思考力を養う必要があると感じました。

スキのない対策が求められる学校ですね。