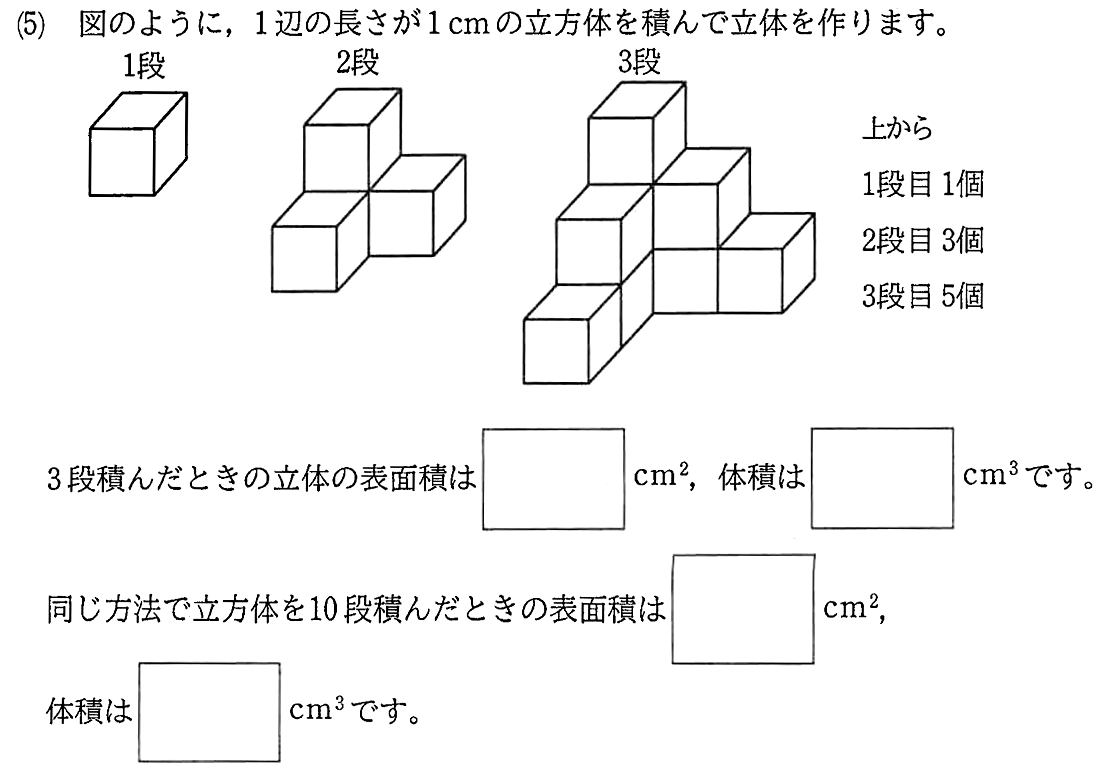
VOL.2841問全力解析 2023女子学院中学校
今回の1問全力解析は2023年女子学院1.(5)です。
まずは問題を見てください。
基本テーマ
①立体をとらえる
②立方体の積木
③規則性を見抜く
④体積の求め方
⑤表面積の求め方
この問題では以上のような基本テーマが潜んでいると考えられます。
ひとつずつ見ていきます。
①立体をとらえる
見取り図を見て全体像がつかめないと正解することはできません。
本問は基本問題なので、どんな形かわかりにくいといったことは無いでしょうが、複雑な問題は何らかの技術を使う必要があるでしょう。
②立方体の積木
立方体の積木は
(Ⅰ)上から見た図に何段積まれているかの数を記入する
(Ⅱ)投影図を描く
(Ⅲ)輪切り方式
等の対処法が考えられます。
本問の場合は表面積は(Ⅱ)、体積は(Ⅰ)か(Ⅱ)が有力だったと思います。
③規則性を見抜く
3段は見取り図がありますが、10段はありません。
10段は自分で何とかするしかありませんが、本問の場合はすんなりいったことでしょう。
上の(Ⅱ)を使えば、正面と側面が三角数(1~10)になっていて上面は「10+9」になっていることがわかります。
④体積の求め方
この手の問題は表面積のほうが厄介なことが多いです。
本問の体積はとても求めやすくなっています。
1つの立方体の体積が1cm3なので、立方体の個数の数字が答になります。
⑤表面積の求め方
厄介な表面積ですが、立方体の積木の表面積の求め方にはは決定版があります。
立方体の積木の表面積
→3方向から見た面積の合計×2
※ただし隠れている部分がある場合はその分を足す必要があります。
本問の場合は(Ⅱ)の投影図を描く、あるいはイメージすることで容易に解決したことでしょう。
以上を踏まえて問題を解いてみましょう。
〈解説〉
3段
ⅰ.表面積
投影図のイメージを頭の中に描き(今回は平易な問題なのであえて図を描かないことにします。)ます。
正面→1+2+3=6
側面→同上
上面→3+2=5
表面積→1×1×(6×2+5)×2=34(cm2)…(答)
ⅱ.体積
それぞれ何個あるのか調べます。
(A)一番奥→1+2+3=6
(B)(A)以外→1+2=3
※(A)の隙間に(B)が入るので(A)+(B)は3×3=9と求めることができます。
体積→1×1×1×3×3=9(cm3)…(答)
10段
解き方は3段のときの考え方がそのまま使えます。
ⅰ.表面積
正面・側面→1+2+3+…+8+9+10=55
上面→10+9=19
表面積→1×(55×2+19)×2=258(cm2)…(答)
ⅱ.体積
1×10×10=100(cm3)…(答)
いかがでしたでしょうか。
すんなり答がでたと思います。
ただ、条件は皆同じですから、正解するのは当たり前、かなり厳しいスピード勝負だったと思われます。
「立体図形」も苦手にしている受験生が多いため、今回も平易な問題を取り上げました。
今の時期は本問のような基本問題でチェックを行い、基本を完成させることが大切だと思います。
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の1題平面図形
難易度★★☆☆☆
〈図1〉
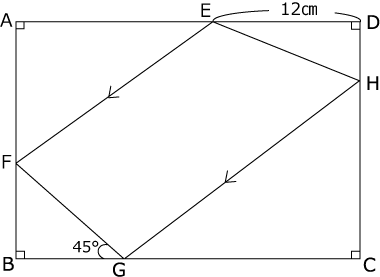
長方形ABCDの辺上に4点E、F、G、Hをとり四角形EFGHを作ると以下のようになりました。
∠FGB=45°
ED=12cm
EF//HG
〈図2〉
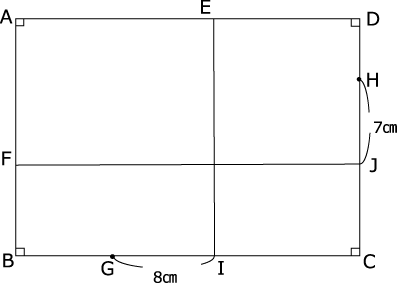
点Eから辺BCに、点Fから辺DCにそれぞれ垂線を下ろしその交点をI、Jとすると以下のようになりました。
GI=8cm
HJ=7cm
〈図3〉
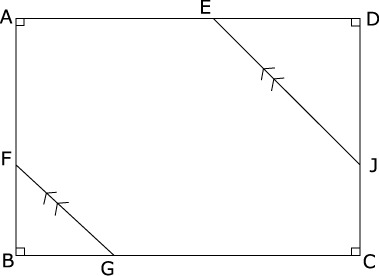
FとG、EとJをそれぞれ結ぶとFG//EJとなりました。
(1)DHは何cmですか。
(2)四角形EFGHの面積は何cm2ですか。
解答が表示されます