VOL.283１問全力解析　2023麻布中学校

今回の１問全力解析は２０２３年麻布２です。
まずは問題を見てください。

この問題では以上のような基本テーマが潜んでいると考えられます。
ひとつずつ見ていきます。

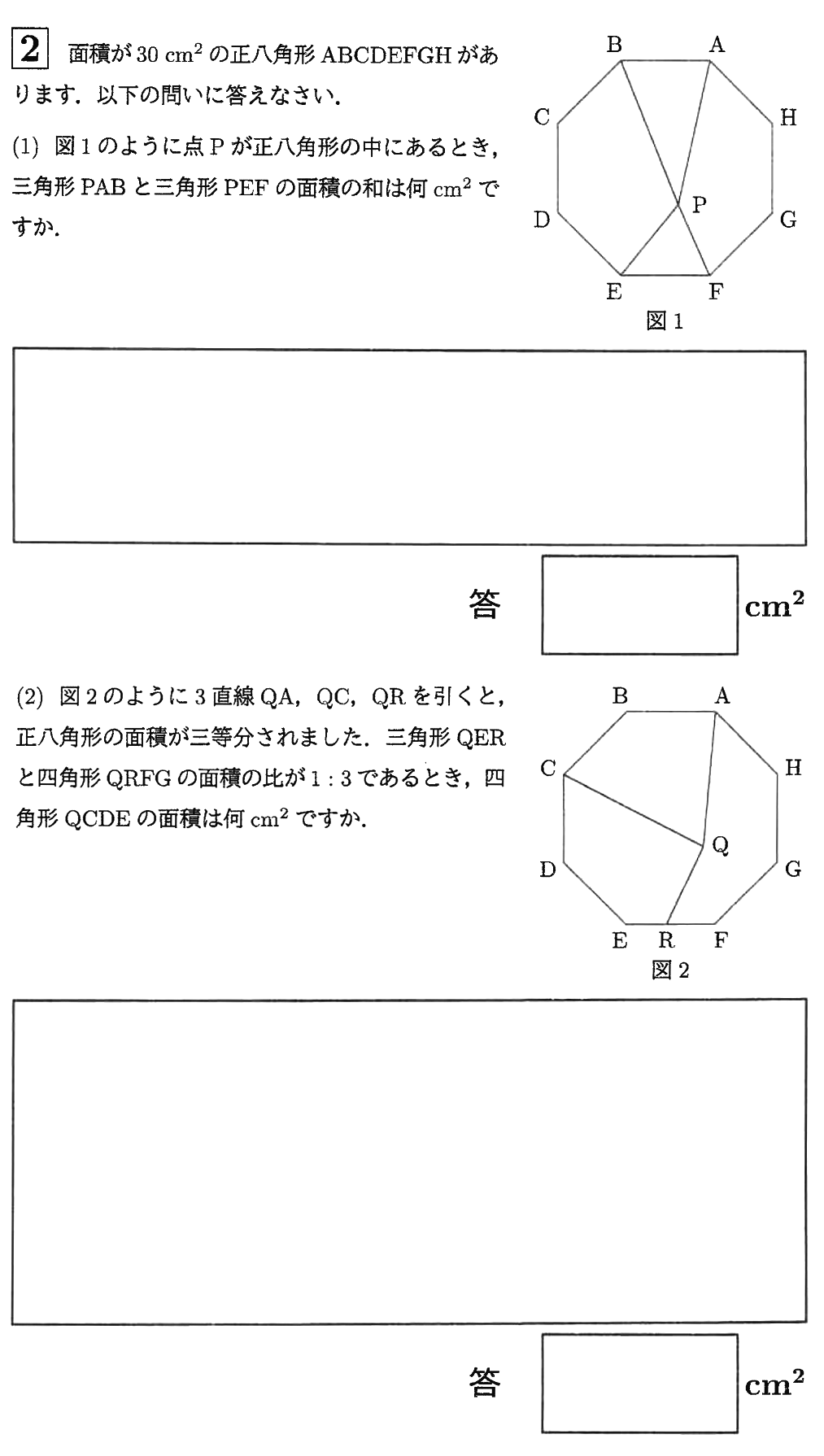
①正八角形の８等分
正六角形では当たり前ですが、正八角形でも下のような分割は良い形になります。

真ん中の点は正八角形の外接円の中心です。
当たり前ですが８個の二等辺三角形は合同です。

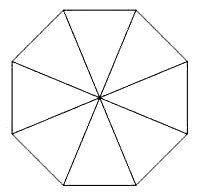
②面積が平行四辺形の半分
これも基本中の基本ですが、下の図の色のついた部分の面積は平行四辺形全体の半分です。

本問は長方形をつくることによって、上を使うことができます。

③（１）が誘導になっている
本問の主眼は（２）だと思いますが、いきなり（２）だとどこから手を付けてよいかわからないような所があります。
このような厄介な問題は（１）が誘導になっていることが殆どですし、実戦的には（１）が誘導になっているものとして扱うべきだと思います。
実際、誘導にはなっているのですがこの後述べる④に気が付かないと、正解にたどり着けなかったかもしれません。
本問からも、本校が最難関校のひとつであることがわかると思います。

④２つ合わせると
（１）と同じようなことは正八角形内に４組ありますから、２組分を合わせれば面積は正八角形の半分になります。
本問の場合やや情報が散乱していますが、うまく処理すると上のように面積が半分の状況をつくることができます。
ここが本問攻略の最大の山場だったと言えるでしょう。

⑤関係式を立てる
算数の場合基本的に「数字」で答を出すので、「図形」といえどもどこかのタイミングで「数字」に変換しなければなりません。
本問の場合は④に気づいた後、関係式を容易に立てることができるので、この段階で「数字」に移行することになるでしょう。
関係式を立てることは答を出すための儀式のようなもので、ここまでくれば正解が完全に視野に入ってきます。
以上を踏まえて問題を解いてみましょう。

〈解説〉
（１）
〈図１〉の長方形ＡＢＥＦの面積は正八角形を８等分した二等辺三角形２個分の倍に等しいです。
〈図１〉

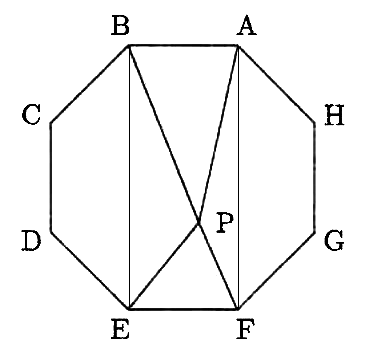
求める面積は長方形ＡＢＥＦの半分なので
３０÷８×２×２÷２＝７．５（ｃｍ^２）…（答）

（２）
〈図２〉のようにＱＥとＱＧを結びます。
〈図２〉

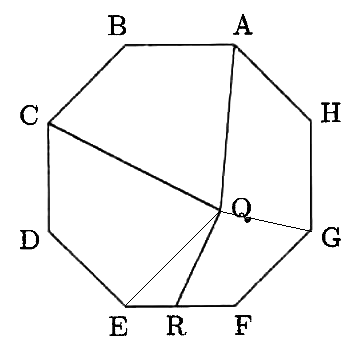
四角形ＡＢＣＱの面積は
３０÷３＝１０（ｃｍ^２）
です。
また、三角形ＱＥＲの面積を①とすれば四角形ＱＲＦＧの面積は③です。
そして上記３つの図形の和は（１）で求めた面積の２倍です。
※〈図３〉参照のこと
〈図３〉

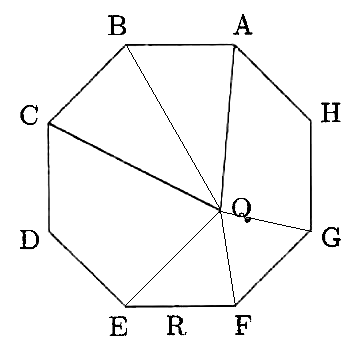
よって、以下の関係式が成り立ちます。
１０＋①＋③＝７．５×２
④＝５
①＝１．２５（ｃｍ^２）
以上より
四角形ＱＣＤＥ＝五角形ＱＣＤＥＲ－三角形ＱＥＲ
＝３０÷３－１．２５
＝８．７５（ｃｍ^２）…（答）

いかがでしたでしょうか。
使っている考え方や知識は基本的なものでしたが、そこに持ち込むところに「力」が必要だったと思います。
この「力」はこのブログで特に初期のころに強調してきた内容です。
算数は「力」をつけておかなければならないことを、この問題でも確認することができました。