VOL.2741問全力解析 2023筑波大附属駒場中学校
3月は新中1生の数学の授業をやることが多いです。
実はこの時期に先取りをすることには、メリットがいくつもあります。
①これからやる数学の全体像を知ることができる
②算数から数学への移行を練習することができる
③算数と数学の相違を感じることができる
④今後おこなわれる学校の試験の対策になる
結果として初期の成績が良好となれば、その後の中学から高校までの学内でのポジションもそのままであることが多いと聞きます。
その後の人生が大きく変わるということが起きるかもしれません。
さて、しばらくは「1問全力解析」をやっていきたいと思います。
今回取り上げるのは2023年筑波大附属駒場中3です。
基本テーマ
①計算力・判断力
②直角三角形の相似
③補助線・折る
④比をそろえる
⑤算数の奥深さに触れる
この問題では以上のような基本テーマが潜んでいると考えられます。
ひとつずつ見ていきます。
①計算力・判断力
本問は図形問題ですが一定以上の計算力が求められます。
本校の受験生ならば全く問題ないレベルではありますが、入試問題は「計算を煩雑にすることによって差をつける」といった手法もあることは知っておくべきでしょう。
また、一定以上煩雑な計算になることが判明した場合はいったん飛ばすという判断が賢明となる場合もあります。
本問の場合はそこまでではないので最後まで解き切ることが正解だったと思われます。
問題によっては、いったん飛ばすべきケースもあるでしょう。
そのあたりの判断を誤らないよう、十分に練習しておく必要があります。
②直角三角形の相似
「図形」は「形」に対して敏感になることが大切です。
「相似」は受験算数において最重要テーマのひとつといっても過言ではありません。
その「相似」が発生しやすいのが「平行」と「直角」があらわれた時で、「直角三角形」はその典型例です。
ですから、直角三角形が出てきた時は相似(さらに言えば合同)を探すことから入り、なければ作る位の積極性が求められます。
本問の場合は「直角三角形を作り相似を利用する」ことで解決します。
③補助線・折る
②で触れたように本問の場合は補助線を引いて直角三角形をつくる必要があります。
(1)は2つの直角三角形をくっつけた形なので補助線は必要ありませんが、(2)は(1)の図形からいの角度を引いたものを作図することになります。
実際は紙を折るような感覚で作図すれば良く、折り紙の問題で鍛えた経験が役にたったことでしょう。
(3)も同様ですが、より折り紙の感覚が求められたように思います。
折り紙は折ったものを開くと合同が生じます。
すると相似な直角三角形を作りやすいということになります。
④比をそろえる
作図が完了すれば実質的には解けているのですが、煩雑な数値との闘いがあります。
要は「比をそろえる」わけですが、単純に最小公倍数にすればよいのか、検討する価値はあるでしょう。
今回は私ならどうするかを一つの例としてご紹介します。
⑤算数の奥深さに触れる
この問題の内容は本当に素晴らしいと思います。
まず、直角三角形の三辺の比が整数になる不思議さがあります。
そして異なる比の直角三角形を2つ組み合わせることによって、元の三角形のうちの一つと相似な三角形を2倍したものができるとは!
こういったことを面白い、もっと色々なことを知りたいと思うのか、何も感じないかで今後の算数・数学の出来が大きく変わってきます。
楽しみながら勉強できれば最高ですね。
以上を踏まえて問題を解いてみましょう。
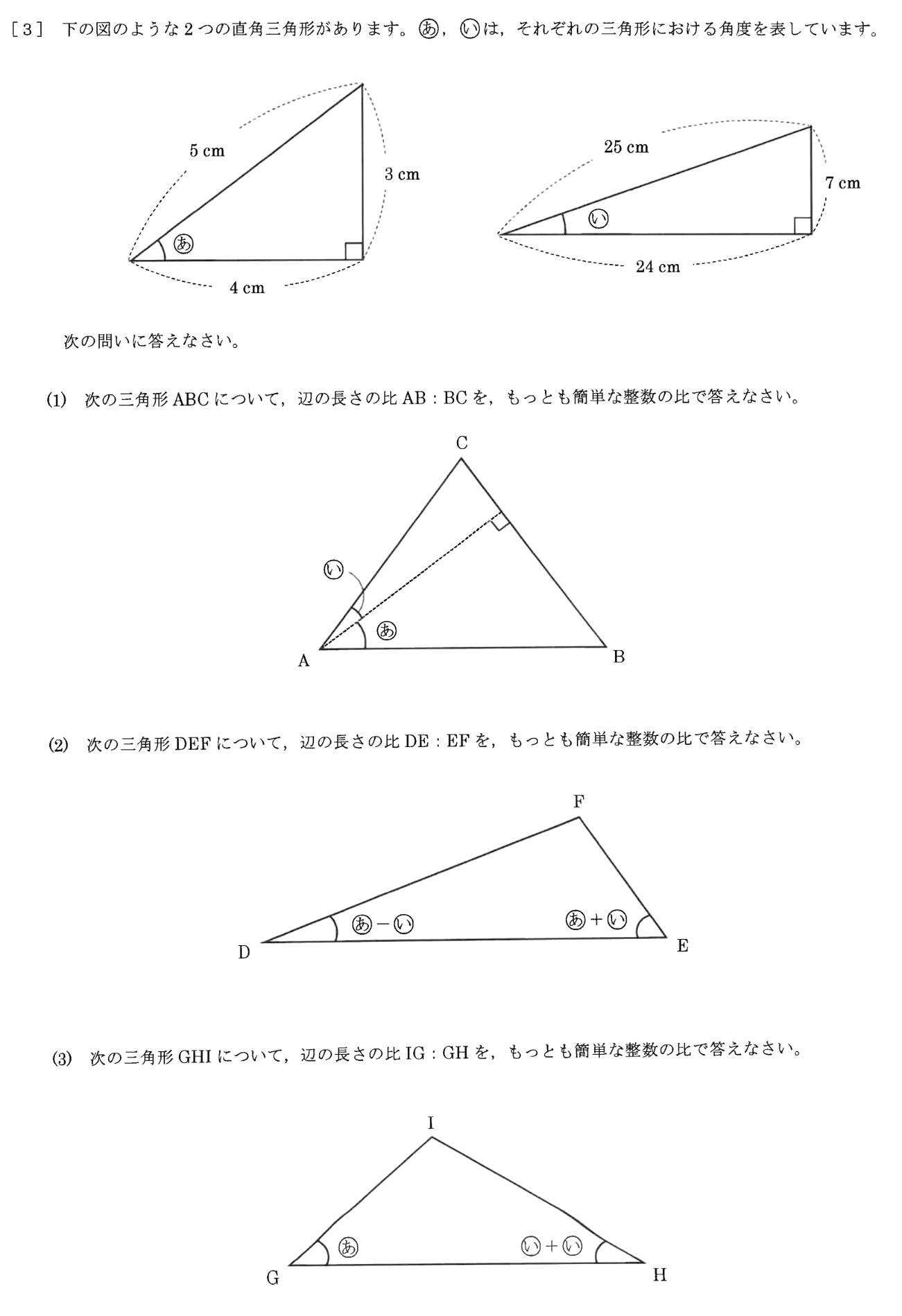
(1)比をそろえれば良いです。〈図1〉に3:4:5と7:24:25を書き入れます。
〈図1〉
4=24 なので
5=30
25:30=5:6・・・(答)
(2)(1)の三角形をもう少し見ていきます。
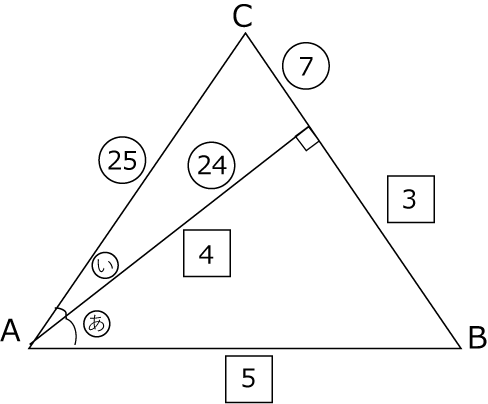
Cから辺ABに垂線を下ろしたものが〈図2〉です。
〈図2〉
AC:AM=5:3
MB:CB=6-3:5
=3:5
より
△CAMと△CBMは合同であることが分かります。
よって
∠A=∠B
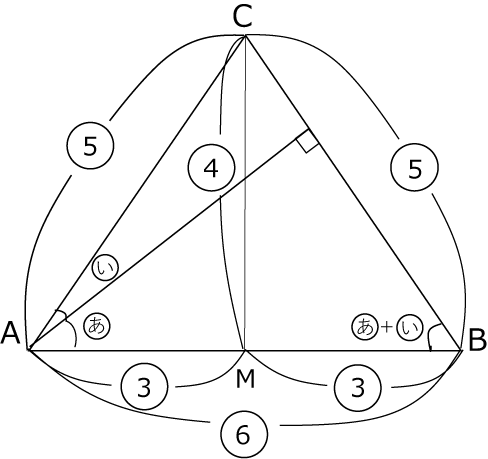
〈図2〉を直線ℓを軸として折り返しを図形が〈図3〉です。
〈図3〉
⇓比を書き込んで
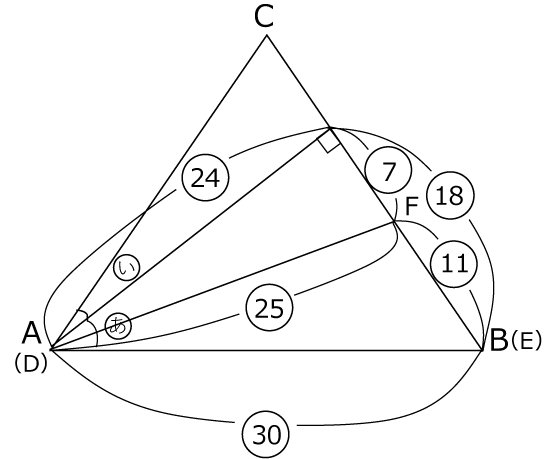
24× 5 4 =30
24× 3 4 -7=11
以上より
30:11・・・(答)
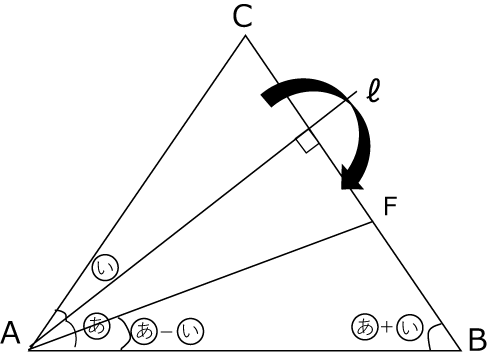
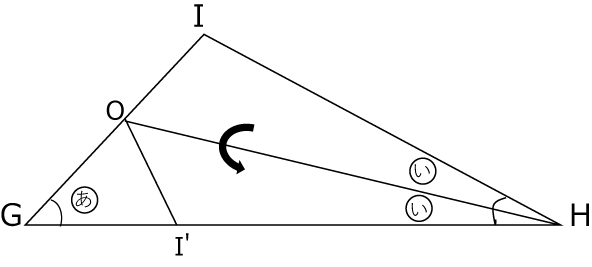
(3)まずは、∠Hを半分に折ります。(〈図4〉)
〈図4〉
IとI´を結びIからGHに垂線を下ろします。(〈図5〉)
〈図5〉
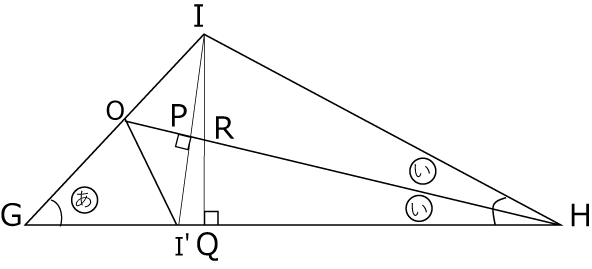
ここで△RQH、△I´PH、△RPI、△I´QIはそれぞれ相似であることを確認します。
比を書き入れてそろえれば終了ですね。
24と25の最小公倍数が600なのでIPを600として比を書き入れます。(〈図6〉)
〈図6〉
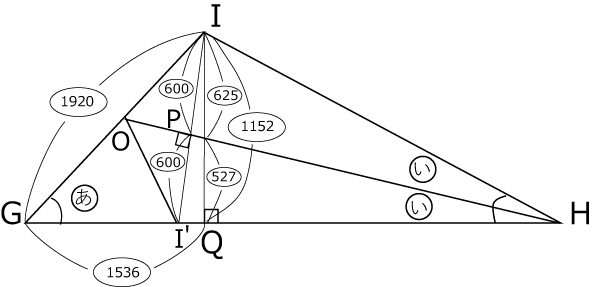
600× 25 24 =625
600×2× 25 24 =1152
1152-625=527
1152× 5 3 = 384×5=1920 ↑これを使います。
1152× 4 3 =1536
QHが求められれば良いので
GH⇒527× 24 7 、
GH⇒1536+ 527×24 7 = 24×(64×7+527) 7 = 24×975 7
384×5= 24×975 7 =7×16:195=112:195・・・(答)
〈別解〉
ここまで書いてきて少し違和感がありました。何か大切なものが欠けている気がしました
基本テーマに以下を加えます。
⑥誘導に乗り図形的性質を見抜く(二等辺三角形の発見)
この姿勢がやや欠けていたことにより、計算の煩雑さを招いたということになります。
(1)、(2)を解いた時点で角度についての情報を整理します。
〈図7〉
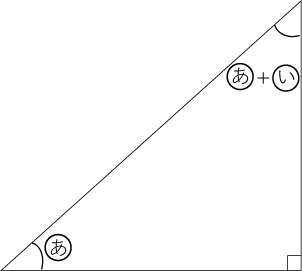
〈図8〉
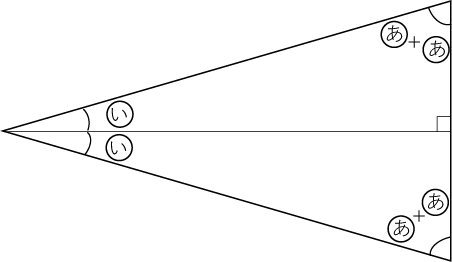
あ+あ+い ⇒ 90°
2倍して
あ×4+い×2 ⇒180°
(3)の図形に〈図8〉の二等辺三角形をはめ込みます。
〈図9〉
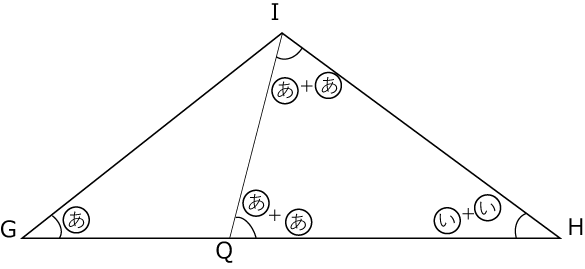
∠GIQ=180°-(あ×3+い×2)
あ×4+い×2が180°なので
∠GIQ=ああ
〈図10〉
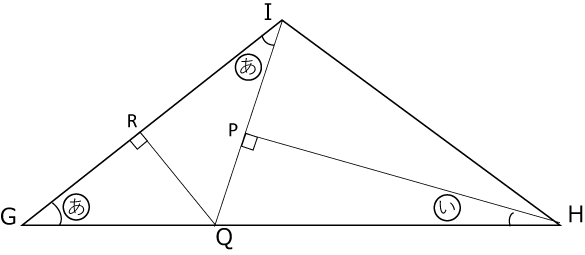
*△IQGは二等辺三角形です。
*二等辺三角形のてっぺんから底辺に下ろす垂線は有効な補助線になることが多いです。
Qから辺IG,Hから辺IQにそれぞれ垂線を下ろせば準備完了です。
〈図11〉
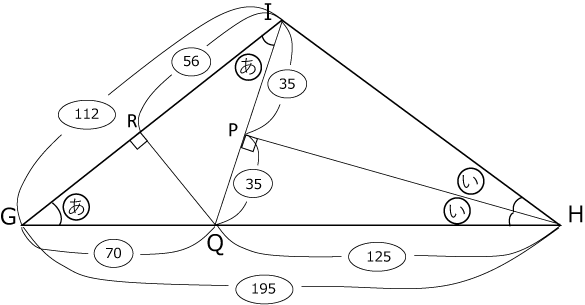
PQを35として比を書き入れます。
35× 25 7 =125
35×2=70
70× 4 5 ×2=112
70+125=195
よって(答)112:195
いかがでしたでしょうか。
折り返してから垂線を引いて相似をつくる問題でした。
過去に類題があるので、解けた受験生が多かったと思います。
最後に計算の煩雑さがありましたが、本校の受験生なら難なく跳ね返したことでしょう。
また、図形的に見抜けていれば、計算の煩雑さは解消され、よりスマートに解くことができました。
これも、数量的な処理よりも図形的な処理を優先した方が得をすることが多いという算数の基本とも言えるものでした。
以上のように、算数の面白さが詰まった問題だったと思います。
この様な問題を解くことを「楽しい」と感じる事ができるかどうかが、今後の学力の伸びに関わってくるのではないでしょうか。
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の1題平面図形
難易度★★★☆☆
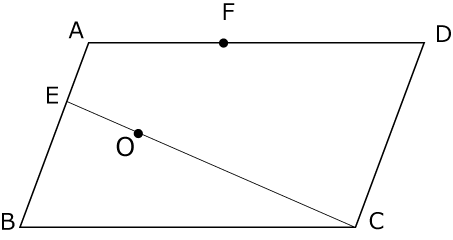
〈図1〉は平行四辺形ABCDの辺AB上に点E、直線EC上に点O、辺AD上にAF:FD=2:3になるように点Fとった様子をあらわしています。
〈図2〉は〈図1〉の平行四辺形に対してAO、FO、DO,FCを直線で結んだ様子をあらわしています。
〈図1〉
〈図2〉
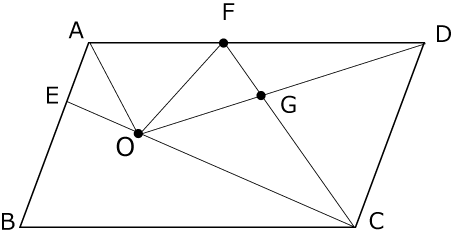
〈図2〉で△AEO、△FOC、△DOCの面積はそれぞれ6cm2、48cm2、84cm2、でした。
(1)平行四辺形ABCDの面積は何cm2ですか
(2)三角形GOCの面積は何cm2ですか?
解答が表示されます