VOL.240数学から考える受験算数(6)平方根
かなり昔、たまたま他の先生が理科の授業を行っている様子が聞こえてきました。
内容は「ふりこ」でした。
先生が「周期が2倍になるのは長さが何倍のときか?」と質問すると、生徒さんが「ルート2倍!」と即答していました。
生徒さんは、小学6年生だったと思いますが、なかなかやるなと思いました。
ただし、受験の観点からは「平方根」を学ぶことは効率が悪いのではと考えていました。
あれから何年も経ちました。
今回は改めて「平方根」を学ぶのが良いか悪いかを検証したいと思います。
「平方根」は中学数学で習いますが、少なくとも「正負の数」「文字式」「式の計算」を学んだ後でないと完全には理解できないと思われます。
ここで「平方根」の定義を確認しておきましょう。
2乗してaになる数がaの平方根(ただしaは正の数)
このことの理解だけなら大半の小学生は5分もかからないでしょう。
先ほどの生徒さんもほとんど一瞬だったことでしょう。
ところが、中学生になり、数学の授業の中でやってみると話はそこまで単純じゃないことを知ることになります。
例えば「5の平方根はいくつですか」と質問すると、初めての生徒さんは経験上半分以上の確率で間違えます。
正解は「ルート5」ではなく「±ルート5」です。
小学生までは「ルート5」でも正解かもしれませんが、マイナスの領域を扱うようになってからは「±」をつけなければいけません。
また、平方根の意味がわかったとしても、根号を含む式の計算は覚えなければいけないことが沢山あります。
・根号を含む式の乗除
・根号を含む式の加減
・分母の有理化
・根号の中の整理
以上のようなことを一通り学ばなければ計算ができません。
そして、その前提として「文字式」を扱えなければならないので、「数学」をきちんと学んで基礎をつくっておかないと「平方根」を扱うことはできないというのが私の結論です。
例をひとつあげましょう。
振り子の問題で振り子の長さと周期が表であたえられる問題があります。
平方根を習えば「長さ1mのときの周期が1秒」とわかれば長さが何mでも周期は求められるのですが…
長さが8mのときの周期を求めてみます(小数第二位を四捨五入)。
長さが8倍になれば周期はルート8倍ですから
1×ルート8
=ルート8
=2.82…
≒2.8(秒)
ルート8の近似値を知っていれば即答級だったでしょうが、普通小学生は知りません。
すると
2×2=4
3×3=9
から2の後ろの方と見当をつけ
2.8×2.8=7.84
2.9×2.9=8.41
から2.8秒とすることが考えられます。
また、ルート8=2ルート2なので、ルート2が1.41…を知っていればその2倍で2.8秒とすることもできます。
いずれにせよ、あまり意味がない(このようなことは小学生には要求されない)と感じました。
皆さんはいかがでしたか?
小学生の場合、正三角形の高さや正方形の対角線の長さがずっと「無視」されるので、それが「ルート3」や「ルート2」のような、いままで習っていない数だと習うのは良いことだと思います。
ただし、あまり深追いすると完全に数学の領域に入ってしますので、「そのような数がある」程度にとどめるのが良いのではないでしょうか。
最後に私の好きな平方根の語呂合わせを紹介して終わりにしたいと思います。
一部私が付け足しました。
ルート6=2.44948974278…
煮よよく弱く無しに菜っ葉
弱火でぐつぐつ煮込んだら菜っ葉が無くなってしまった光景が頭に浮かびますね(笑)
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の1題ピタゴラスの定理
★★☆☆☆
「ピタゴラスの定理」という直角三角形の性質が知られています。
〈図1〉
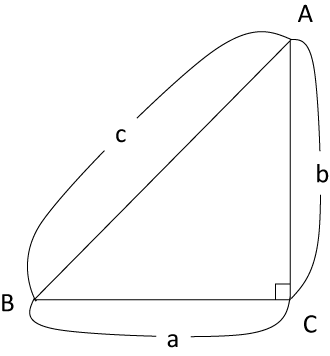
〈図1〉の直角三角形ABCにおいて
a×a+b×b=c×c
が成り立つというものです。
〈図2〉
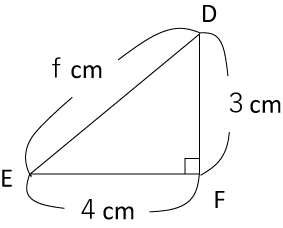
例えば〈図2〉では
f×f=3×3+4×4
=25
なので、fは5(cm)だという事がわかります。
〈図3〉
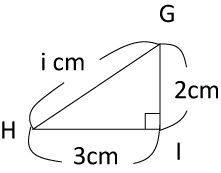
ところが、〈図3〉は
i×i=2×2+3×3
=13
となり、同じ数を2回かけて13になるものは「九九」の中にありません。
そこで、2回かけ合わせて13になるような正の数を[13]とあらわすことにします。
[ ]の数の計算は以下のようになります。
[2]×[2]=2、[5]×[5]=5
[2]×[3]=[6]、[3]×[7]=[21]
[2]×[6]=[2]×[2]×[3]=2×[3]
[8]×[18]=12
〈図4〉
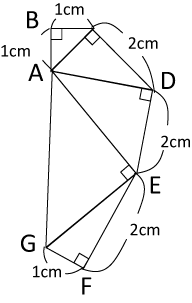
〈図4〉は辺と辺が重なるように5つの直角三角形を並べたものです。
以下の問いに答えて下さい。
(1)AGの長さは何cmですか。[ ]を使って答えて下さい。
(2)AD×AE×AGを求めてください。
解答が表示されます













