VOL.234一問全力投球(17) 栄光学園中
今週の「1問全力投球」は神奈川の名門校「栄光学園」です。
2022年度の1を取り上げます。
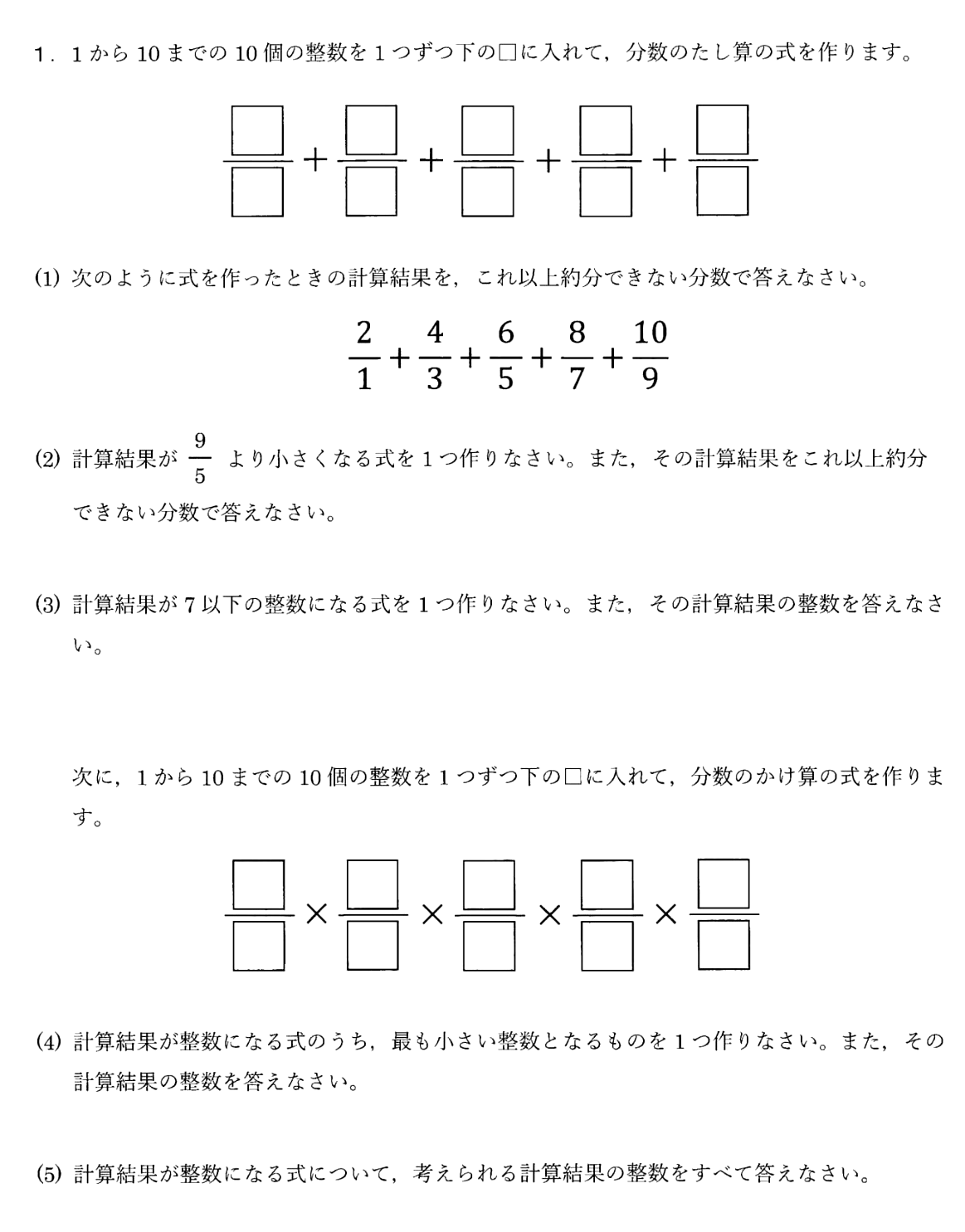
まずは問題を見てください。
今年度の「栄光学園」はかなりハードな内容でした。
普通に考えると半分取れれば御の字、大きく崩れてしまった受験生もいたのではないでしょうか。
かなりの受験生の躓きの原因がこの1にあったと推測されます。
やはり、出鼻をくじかれると辛いものがあります。
今回はたまにある1が手ごわい時の対策も考えながら解説を進めていきたいと思います。
〈解説〉
本校や「麻布」等で頻出の「指定された数を作るタイプ」の問題ですね。
問題によって「全てを調べる」か「的を絞って調べる」かのどちらかを選択する必要があります。
どちらにせよ「思考力」をみたいという学校側の意思が感じられます。
(1)まずは計算です。
足し算ですので帯分数にしてから計算すべきでしょう。
その後分母を5と7と9の最小公倍数である315にそろえれば間違えることはないでしょう。
(答)6 248 315
(2)この問題は1つ作ればよいのがポイントです。
確実に 9 5 より小さくするには一番小さいものを書けばよいのですが、その後の計算が煩雑になります。
分母を大きくした後はなるべく計算が簡単になる分数の足し算にするのが得策でしょう。
まずは一番小さいものを書き、それに少し変更を加えて計算が簡単になりそうなものを作ります。
この発想がない場合は(3)は早めに切り上げ、(4)に進んだ方が良かったかもしれません。
最小… 1 6 + 2 7 + 3 8 + 4 9 + 5 10
簡単… 1 6 + 2 7 + 4 8 + 3 9 + 5 10
分母が8と9のところの分子を入れ替えただけですが、計算は格段に簡単になりました。特に、 1 2 と 1 3 を足すと 5 6 ですが、それと 1 6 との相性が良く、
1+ 2 7 + 1 2 =1 11 14
と簡単に計算でき、これは 9 5 より小さいことから答として使えますね。
(例)
1 6 + 2 7 + 4 8 + 3 9 + 5 10
計算結果…1 11 14
(3)上の計算が使えそうです。
「7」がネックになりそうなので分子側にもってくるとすると
7 6 は1 1 6 なので「7」と「1」を入れ替え
7 6 + 2 1 + 4 8 + 3 9 + 5 10
計算結果…4.5
となり、かなり整数に近付きました。
「2」と「1」か「5」と「10」を入れ替えれば整数になりますね。
(例1)
1 2 + 7 6 + 4 8 + 3 9 + 5 10
計算結果…3
(例2)
2 1 + 10 5 + 7 6 + 4 8 + 3 9
計算結果…6
(4)ここから掛け算になるのですが、これは類題を見たことがあります。
1~10まで素因数分解しましょう。
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 2×2 |
| 5 | 5 |
| 6 | 2×3 |
| 7 | 7 |
| 8 | 2×2×2 |
| 9 | 3×3 |
| 10 | 2×5 |
素数の数をカウントすると
2 8個
3 4個
5 2個
7 1個
となっているので、理論上最小値は「7」となります。
あとはそのようなものが作れるかですが、結論から言うと作れます。
以下は解答例です。
(例)
3 1 × 5 2 × 6 4 × 7 9 × 8 10
計算結果…7
(5)全部なので苦しいですが、頑張ってみます。
場合によっては見切りをはやくし、先に進んだ方が良かったかもしれません。
7は必ず分子に残るので、計算結果が7の何倍になるかという観点で調べていきます。
また、計算結果が最大となるのは下の式です。
10 5 × 9 4 × 8 3 × 7 2 × 6 1 =7×36
このことから、36倍までを考慮すればよいことがわかります。
2・3・5は全て偶数個使われているので、それぞれ(4)の状態と比べて1つ分母側から分子側へ移れば4・9・25(倍)になります。
2だけ2個移ったときの16倍の可能性があり、4倍と9倍の組み合わせの36倍は既に書きました。
最後は可能かどうかの確認です。
・1倍
3 1 × 5 2 × 6 4 × 7 9 × 8 10
計算結果…7
⇒7×1=7
・4倍→「1倍」の(3,6)と(4,9)を入れ替える
⇒7×4=28
・9倍→「1倍」の(3)と(9)を入れ替える
⇒7×9=63
・16倍→「1倍」の(3,5,6)と(4,9,10)を入れ替える
⇒7×16=112
・25倍→「1倍」の(3,6)と(9,10)を入れ替える
⇒7×25=175
・36倍→上記の最大値
⇒7×36=252
以上より
(答)7,28,63,112,175,252
いかがでしたでしょうか。
本問は(3)で沼にはまってしまうとなかなか抜け出ることができず、全部をダメにしてしまう可能性すらあったと思います。
1番は普通は点数を取りやすいことが多いですが、難問が配置されることもあります。
最初の問題だからこそ、見切りをはやくする「勇気」が必要と言えるでしょう。
また、本問は(3)に関しては「的を絞って調べる」姿勢が良く、(5)に関しては「全てを調べる」ような気持ちが必要でした。
その点からも一筋縄ではいかない入試問題だったと言えると思います。
とは言え、本ブログで普段から書いていることを実践してもらえれば、十分に対応可能だったのではないか、と金田は妙に納得しているのでありました。
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の1題図形
難易度★★☆☆☆
(1)正方形を縦に917個、横に1441個並べて長方形を作ります。そこに対角線を1本ひくと、対角線は何個の正方形を通りますか。
(2)立方体を48×80×120(個)のように並べて直方体を作りました。そこに長さが最大になるように頂点と頂点を直線で結びました。その直線は何個の立方体を通りますか。
解答が表示されます