VOL.232一問全力投球(15) 広尾学園中
今週は共学の人気校「広尾学園」をとりあげます。
本校の特徴が良くあらわれている3を選びました。
まずは問題を見てください。
頻出の問題と言えますが、(3)が応用問題となっています。
その応用の加減がいかにも本校らしいと感じたので、ここで取り上げた次第です。
〈解説〉
(1)はやってみましょうという意図でしょうが、学習済みの受験生にとっては通い慣れた道のようなものだったでしょう。
《123》=123+132+213+231+312+321=1332 …(答)
上の考え方で問題ないとは思いますが、やはり計算で求められるようなやり方も押さえておきましょう。
3つのものの並べ方は順列で大丈夫なので
3×2×1=6(通り)
使っている数字の数、それぞれの桁(百の位・十の位・一の位)の数字の数は
3×6=18,18÷3=6
「1」「2」「3」の平均は
(1+2+3)÷3=2
以上より
(2×100+2×10+2×1)×6
=12×111
=1332
ポイントは「1」「2」「3」が同じ回数だけ使われるということですね。
この時点で公式化が可能です。
Nが3桁の場合の《N》
①Nが1種類の数字からなる場合(mmm)
《N》=N
②Nが2種類の数字からなる場合(mmn)
《N》=(m×2+n)÷3×111×3
③Nが2種類の数字からなる場合(mno)
《N》=(m+n+o)÷3×111×6
②、③の式の意味は、3数の平均に桁の意味する数字をかけ、作れる個数をかけたものです。
(2)Nが3桁であることは明白です。ですから上の公式の①か②か③なのですが、それぞれ検討します。
ⅰ)①の場合
N=777 …1通り
です。
ⅱ)②の場合
(m×2+n)×111=777
なので
m×2+n=7
(m,m,n)→
(1,1,5) …3通り(115,151,511)
(2,2,3) …3通り(221,232,322)
(3,3,1) …3通り(331,313,133)
ⅲ)③の場合
(m+n+o)×111×2=777
m+n+o=777÷2
となり、m,n,oはどれも1桁の整数なので、③の場合はないことがわかります。
以上の検討により
1+3×3=10(個)
(3)ここまでくると、③の場合がありそうだなという予想が立ちます。
Nが4桁ではないことがすぐわかるので、こちらもNが3桁として検討します。
ⅰ)①の場合
なし
ⅱ)②の場合
(m×2+n)×111=1332
なので
m×2+n=12
(m,m,n)→
(2,2,8) …3通り(228,282,822)
(3,3,6) …3通り(336,363,633)
(5,5,2) …3通り(552,525,255)
ⅲ)③の場合
(m+n+o)×111×2=1332
m+n+o=6
(m,n,o)→(1,2,3) …6通り→(1)で確認済
以上の検討により
3×3+6=15(個) …(答)
最後は(1)がヒントになっているというオマケ付きでした。とても親切な設問ですね。
このように「解いてくださいね」という親心のようなものが感じられる入試問題も沢山あります。
頻出なのですが、ほんの少しひねってあるのが本校の特徴であり、そこが越えなければならない壁であると言えます。
本問の場合は使う文字の種類が1~3まであり、そのあたりのことが問われていました。
しかし、例と(1)で1~3種類までのすべてに触れることができるので、(2)、(3)ではそれを生かせるかどうかで明暗が分かれたといえましょう。
受験生の皆さんにおいては、このような中学・高校の先生の期待に応えるべく、しっかりと準備して受験に臨めるよう頑張りましょう。
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の1題整数
難易度★★☆☆☆
異なる2つの整数M,Nに対して以下の(ルール)によって<M,N>を求めます。
ただし、M>Nとします。
(ルール)
ある整数をMで割った時のあまりをm、Nで割った時のあまりをnとする。
(m,n)の組み合わせは いくつか考えられるが、それぞれの組み合わせにつき そのあまりを満たす0以外の最小の整数を全て足したものを<M,N>とする。
例として<3、2>を求めてみます。
あまりの組み合わせと そうなる最小の整数を表にまとめると以下になります。
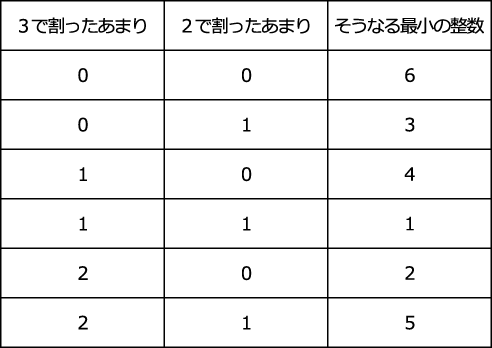
よって
<3,2>=1+2+3+4+5+6
=21
です。
(1)<8,6>を求めて下さい。
(2)<M,N>=78となるようなMとNの組を(5,4)のような形で全て求めて下さい。
解答が表示されます
(1)300
(2)(4,3)、(6,4)、(12,1)、(12,2)、(12,3)、(12,4)、(12,6)














