VOL.231一問全力投球（１４）　筑波大附属駒場中

今回の「１問全力投球」は筑波大附属駒場中を取り上げます。
本校も前回取り上げたＪＧ同様に「時間」が厳しいです。
それに加え、いわゆる「思考力系」の出題もあるので、十分な対策を行っておく必要があります。
本年も「らしい」問題が並んでいましたが、その中から［２］を取り上げたいと思います。

人によっては易しいと感じたかもしれませんが、（３）を理論的に正解までもっていくのはそれなりに大変と判断しここで取り上げました。

〈解説〉

（１）図②の交差点４－ア、４－イ、４－ウの３つの交差点全てに対し２ｋｍ以内の交差点が２人目の警察官を配置できる場所です。

交差点４－アと４－ウだけ考えればよいので、すぐに交差点３－イ、４－ア、４－イ、４－ウの４か所であることがわかります。
（答）　４か所

（２）図③の交差点２－イに１人目を配置したとします。
この位置は左上のコーナーをカバーできる位置の中で、最も内側に入っています。コーナーはあと３つありますが、後１人で全部はカバーできません。
２人でカバーすることは容易（例えば３－エと４－ウ）なので３人が答であることがわかります。

２人では無理なことを別の角度から考えてみます。

２人で４つのコーナーをカバーするには２つずつカバーしなければなりません。
２つのコーナーをカバーできるのは外側の辺上ですが、そうするとどうやっても２人で全部をカバーすることはできません。
例えば交差点１－イと４－ウ、１－イと４－イのどちらもだめです。

（答）　３人

（３）１辺が１４ｋｍの正方形です。道が１５本と奇数なので、正方形の真ん中に交差点があることを押さえておきます。

正方形の真ん中に警察官を配置することを考えます。
その正方形の頂点まで行ければその正方形全部をカバーできることは明白です。
１辺が８ｋｍの正方形の真ん中から頂点まではちょうど８ｋｍです。

１辺が８ｋｍの正方形を４つ並べれば、１５本×１５本の道は全て覆うことができるので、答は８（ｋｍ）以下です。

ここで４人でどの範囲をカバーすれば良いかを考えます。
４つのコーナーを１人ずつでカバーするならば、ちょうど真ん中の交差点も同時にカバーする警察官が少なくとも１人いなければなりません。

コーナーと真ん中の両方を７ｋｍの範囲でカバーできる交差点はいくつか（２８か所）ありますので、答は７（ｋｍ）である可能性が高いです。

コーナーと真ん中の両方を６ｋｍの範囲でカバーできる交差点はありません。また、コーナー２つを６ｋｍの範囲でカバーできる交差点もありませんから、答は７（ｋｍ）以上です。

ここまでで
（答）　７

とやっても良いと思いますが、実際にできるかどうか書いてみることにします。

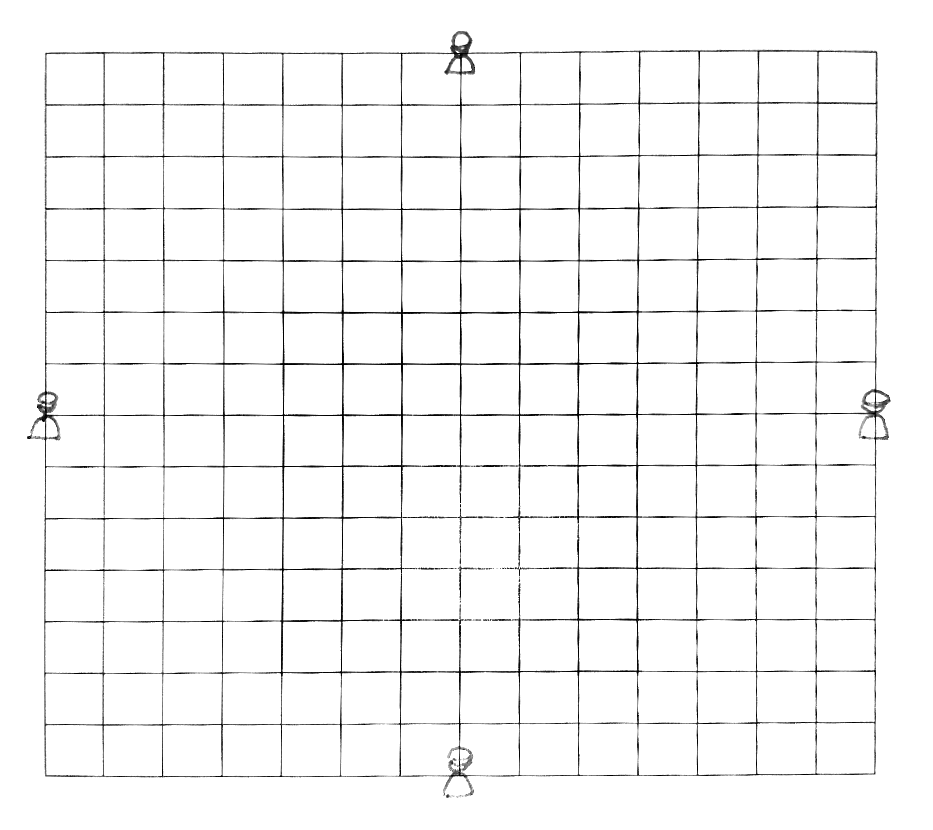
できました！
１つできれば十分ですから、これで大丈夫です。

いかがでしたでしょうか。
コーナーをカバーしなければならないことに着目すれば４人との関連も強いですから、正解にたどり着けたことと思います。

尚、実戦的には、８（ｋｍ）では簡単過ぎますし、少し余っている感覚があるので、答は７
（ｋｍ）だろうと見当をつけるのは有りだと思います。

本年度は［１］と［３］が頻出の問題だったので、この［２］（３）が合否を分けた問題だったかもしれませんね。