VOL.221１問全力投球（７）　灘中

今週の「１問全力投球」は先週に続き「灘中」を取り上げます。
前回は「２日目」でしたが、今回は「１日目」２０２１年５を取り上げます。
問題を見てください。

今回この問題を取り上げたのは、知っていると便利な考え方を紹介したかったからです。
「あまり」については「あまりだけの計算」をすれば良いことは皆さんご存知だと思います。

例えば「５で割って３あまる数と５で割って４あまる数の積を５で割るといくつあまりますか」という問題は

（３×４）÷５＝２…２

より、答は「２」となります。
ところが、

５で割って３あまる数⇔５の倍数－２（２不足）
５で割って４あまる数⇔５の倍数－１（１不足）

とみることができ、「不足×不足」で答が出てしまうのです。

２×１＝２

で良いので、計算が楽です。
結論から言うと不足の個数が偶数個の場合はこのやり方が成り立ちます。

なぜそうなるのか２個のときで説明します。

〈「Ｎの倍数－Ａ」と「Ｎの倍数－Ｂ」の積をＮで割ったときのあまりが「Ａ×Ｂ」となることの説明〉

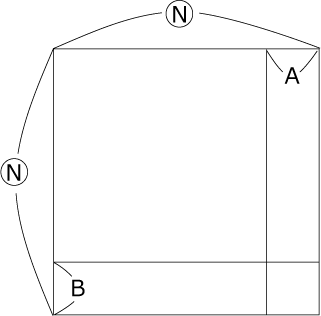
〈図１〉は「Ｎの倍数－Ａ」と「Ｎの倍数－Ｂ」の積を面積図にしたものです。
内側の長方形を１５で割ったときのあまりが「Ａ×Ｂ」になることを示していきます。

〈図１〉

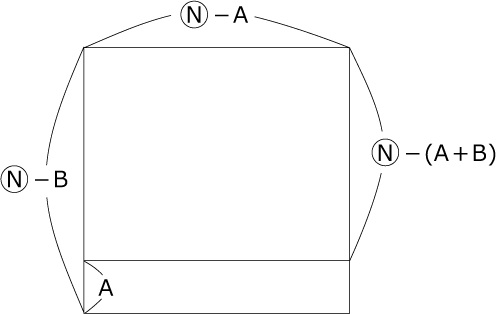
〈図２〉は先ほどの内側の長方形に１本の線を加えたものです。
さらに、下の長方形を切り取り右側にくっつけたのが〈図３〉です。

〈図２〉

〈図３〉

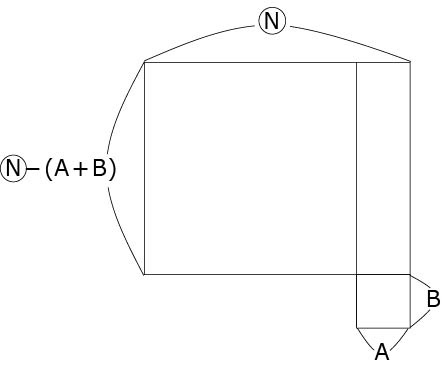
すると、右下の出っ張りの飛び出た部分の縦が「Ｂ」ということがわかります。
横がＮの倍数なので、あまりが「Ａ×Ｂ※」であることがわかります。
※厳密に言えば「Ａ×ＢをＮで割ったときのあまり」です。

これを踏まえ、問題を解いてみましょう。

〈解説〉
「１５で割ったときのあまり」を２回掛け合わせたものを１５で割ったときのあまりを「１～７」について調べます。
あまりが「８～１４」までは「７不足～１不足」に対応しているので、「１～７」の結果を使うことができます。

上の表からあまりが「１」になるのは「１、４、１不足、４不足」の４パターンあることがわかりました。別の言葉で言うと

・１５で割って１あまる　　　　　→　１５×Ｎ＋１
・１５で割って１あまる　　　　　→　１５×Ｎ＋４
・１５で割り切れるには１不足　　→　１５×Ｎ－１
・１５で割り切れるには４不足　　→　１５×Ｎ－４

となります。
このような２桁の数が何個あるか、というのがこの問題です。

２桁の１５の倍数は「１５～９０」の６個ありますが、それぞれに±１、±４したものがとりあえず、２回掛け合わせて１５で割ると１あまる数です。

「２桁」という条件を満たすかどうかのチェックをしなければいけませんが、すべて２桁の範囲に収まります。
よって

６×４＝２４（個）　…（答）

いかがでしたでしょうか。

この問題は本校の受験生にとってはやさしかったでしょうし、
「マイナス×マイナス＝プラス」
を知っていれば面積図は不要だったかもしれません。

ただ、ここに書いた考え方はかなりスマートで参考になったのではないでしょうか。
ぜひ使いこなせるようになってください。