VOL.222１問全力投球（８）　開成中

今週は「開成」を取り上げます。２０２１年３です。

今年のセットは大問３題で、１が小問集合でした。
小問は数字がやや大きいものの論点は頻出なものが２題、基本問題が１題、なぜそうなるのかまで突き詰めると難問であるものが１題でしたので、３問正解はある程度計算できました。

２が「立体図形」で三角すいの体積を求めるものでしたが、本校の受験生ならば３つ取りたい問題でした。これも他校で類題の出題例がありました。

そして、本問となります。
リード文が長く、いかにも「思考力」が要求されるような問題に見えます。

実際は他の問題との兼ね合いで、完答出来なくても合格に必要な点数には届きそうだったため、（３）まで解いて逃げるという戦略もあったと思います。　

では、私ならどうするか！
解説していきます。

〈解説〉

（１）「まずは、やってみよう」という問題です。問題の例と同じように書けば良いのですが、後のことも考えて少し改良してみます。
Ａ君、Ｂ君、審判、スコアスペースを縦に並べ、右から埋めていきます。審判だけ持っている数字ではなくもらった数字を書くようにします。

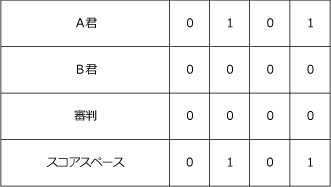
（答）０１０１

（２）「まずは、やってみよう」第二弾です。

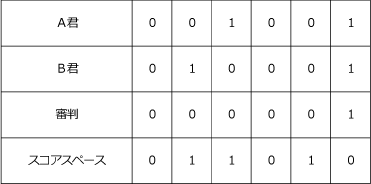
（答）０１１０１０

（３）ここから逆算です。
まずは分かっている部分を表にしましょう。
Ｂ君が６点取るためにはスコアスペースに「１」が６個並び、１番左の審判が「０」でなければならないことに注意しましょう。

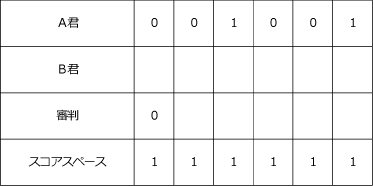
右から埋めていきますが、最初の審判は「０」なので１番右はＢ君も審判も「０」です。
以下同じ要領で表を完成させると下のようになります。

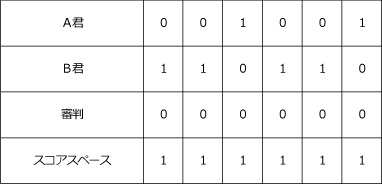
（答）１１０１１０

（４）ここからが本番です。どうやら答が１つではないようです。
ここまで、色々とやってきてきたので、本質に迫っておかなければなりません。
Ａ君とＢ君の「１」の行方ですが、必ず審判かスコアスペースに行くことをしっかりと認識しておきましょう。
そして、審判の一番右が「０」になることも重要で、このことにより表中の数字が
　Ａ君＋Ｂ君＝審判＋スコアスペース
になるわけです。
また、審判はＡ・Ｂ君の「１」を必ずどこかのタイミングでスコアスペースに吐き出すことも意識しましょう。
そうすると今回はＡ君の「１」が２回あるのに得点は「１点」なので、右の１点を審判が抱えた状態で左の１点のところまで行くことが確定します。
また、右から４番目のスコアスペースが「１」だとするとＢ君「１」、審判も「１」になりますが、そうすると審判の「１」が得点として増えてしまうので不可です。

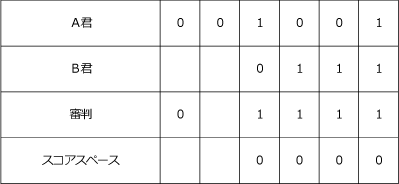
ここまでくると、どちらで１点取るかだけの問題になるので、
（答）０００１１１，０１０１１１

（５）ここまでの経験を活かします。
Ａ君の２つの「１」をどのタイミングで回収するかなので、左３回と右３回に分かれる場合は
　３×３＝９（通り）
あります。

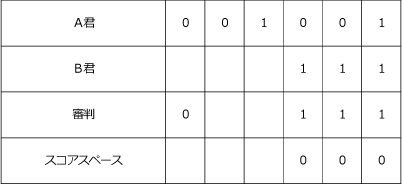
上のように左３回で回収しなければならなくなったケースは３通りなので、
９＋３＝１２（通り）・・・（答）

最後はあっさりとなってしましましたが、本質を見抜けるとこんなものなのかもしれませんね。

本年もこのブログを読んでいただきありがとうございました。
現６年生向けの内容は今回で最後とさせていただきます。

受験生に一言。

「全力投球！」

来年からは現５年生向けとなります。
私なりに良い内容のものを皆様にお届けしたいと考えています。

どうぞご期待ください！