VOL.2201問全力投球(6) 灘中
今週の「1問全力投球」は「灘2日目」2021年2を取り上げます。
問題を見てください。
規則性の問題です。
偶数の個数を最後まで聞いているので、奇数か偶数かの区別がつけば良いことに気づいてください。
一定数の受験生がまともに足し算して終了となったと推測されます。
また、この問題はちょっとだけ見方を変えるだけで有名問題と同じになるので、そこがポイントだったと思います。
ただ、全部書いたとしても
32×32=1024
なので、ギリギリ「書き出し」もアリだったと思います。
それでは私流の解き方を見ていただきましょう。
〈解説〉
結論を先に言っておきます。
この表は斜めに見れば「パスカルの三角形」と同じになります。
また偶数の並びがフラクタル構造になっていて、シェルピンスキーのギャスケットと呼ばれる図形と同じです。
フラクタルとは簡単に言うと図形の部分と全体が相似になっているものをいいます。
〈シェルピンスキーのギャスケット〉

実際は以上のようなことを事前に知っているわけではないので、まずは4×4のマスで偶数の場所をしらべます。
奇数+奇数=偶数
偶数+偶数=偶数
奇数+偶数=奇数
に留意して表を作ります。
ここでは奇数を1、偶数を0で表すことにします。
ここでこの表を対角線で〈図1〉のように2つに分けます。
左上の方が右下よりも1大きい三角数で分けるようにします。
そこに書いてある数字は偶数の数です。
〈図1〉4×4
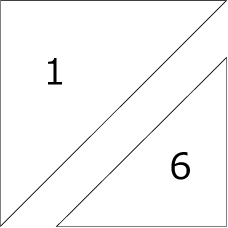
ここで注目したいのは右下の三角形は全て偶数になることです。
また、その偶数の三角形の1段下は全て「奇数+偶数」になりますから、奇数ということになります。
全部奇数だと1番上と同じですから、同じことの繰り返しのようなことになると予想されます。
ただし、斜めに全部奇数が並ぶと、その右下が全部偶数になりますから、1辺が4、8、16、32と2倍・2倍・・・と大きくなっていく正方形の右下部分は全て偶数になります。
以下、〈図2〉から〈図4〉までを掲げます。
〈図2〉8×8
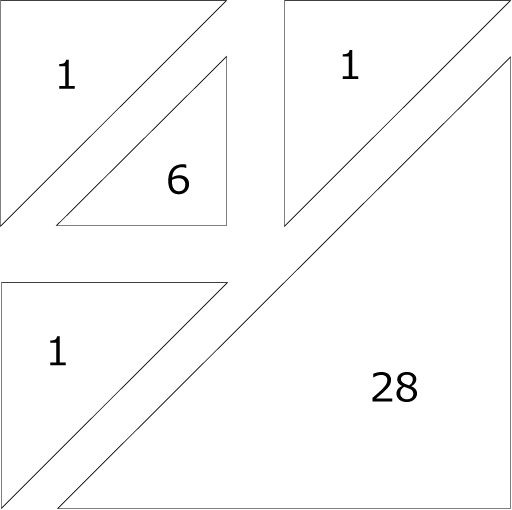
〈図3〉16×16
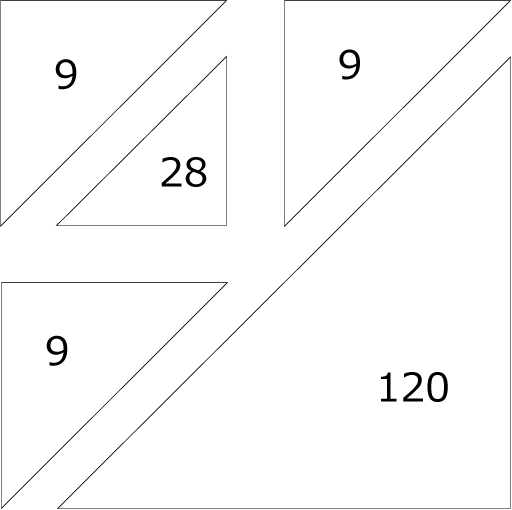
〈図4〉32×32
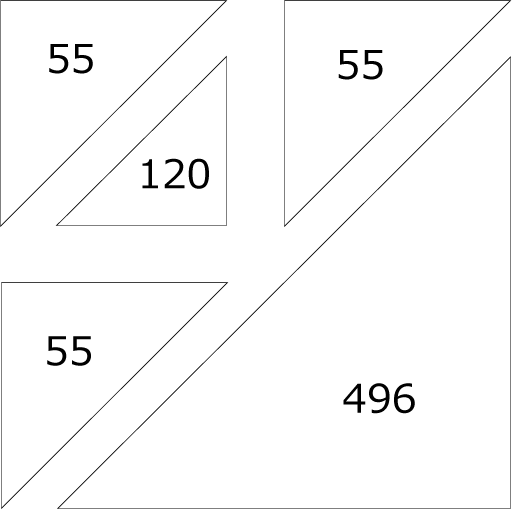
(1)
〈図2〉より、
1×3+6+(1+7)×7÷2=37(個) …(答)
(2)
〈図3〉より
9×3+28+(1+15)×157÷2=175(個) …(答)
(3)
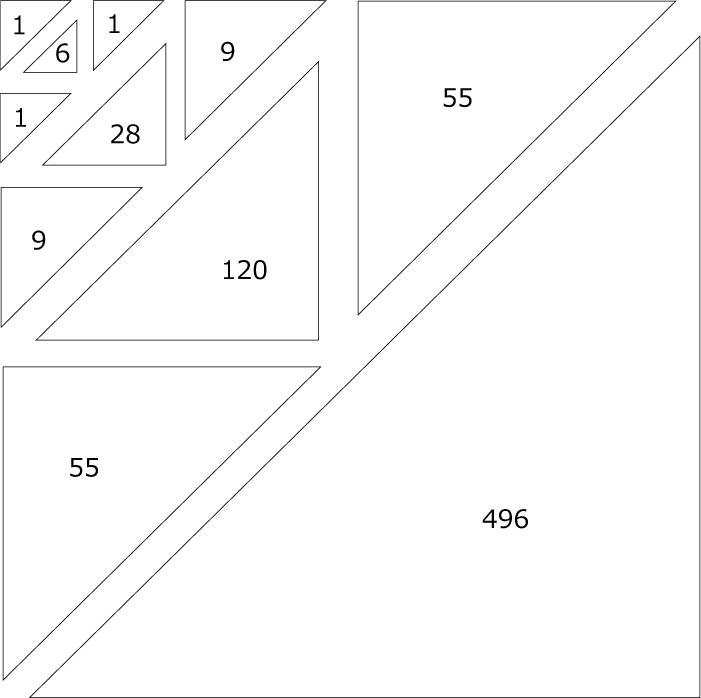
〈図4〉より
55×3+120+(1+31)×31÷2=781(個) …(答)
私は類題を解いたことがあったので短時間で解けましたが、受験生はどうだったでしょうか。
絵を描くようにして解ければ、ライバルに差をつけることができたかもしれませんね。
最後に(1)~(3)に対応できるものを〈図5〉に掲げておきます。
〈図5〉
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の1題平面図形
難易度★★★☆☆
名門君が〈図1〉のような作図をしました。
〈図1〉
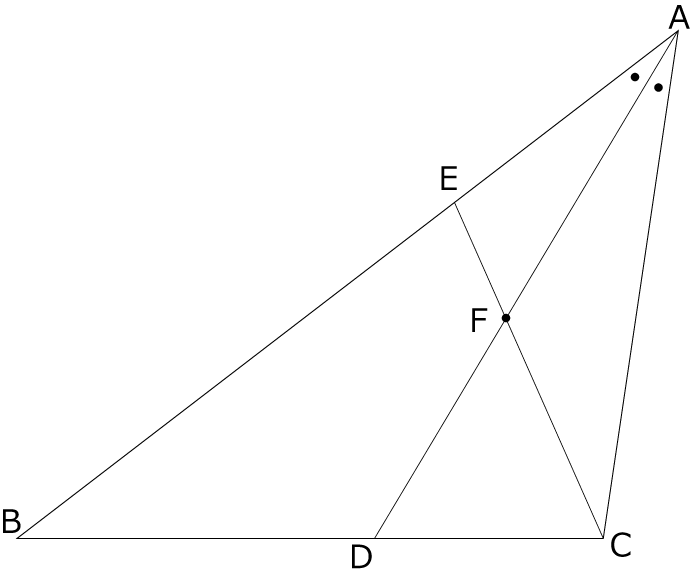
AE=9㎝
EB=18cm
BD:DC=3:2
∠BAD=∠CAD
EF=4㎝
作図後、分度器で∠ACEをはかったら26.5°でした。
以下の問いに答えて下さい。
(1)ACの長さは何cmですか。
(2)∠BCEを分度器ではかると何度ですか。整数で答えて下さい。
解答が表示されます














