VOL.202比を利用しよう(2)
【比を利用しよう】の2回目です。
今回から少し実例を見ていただこうと思います。
煩雑さを削減することが今回のテーマです。
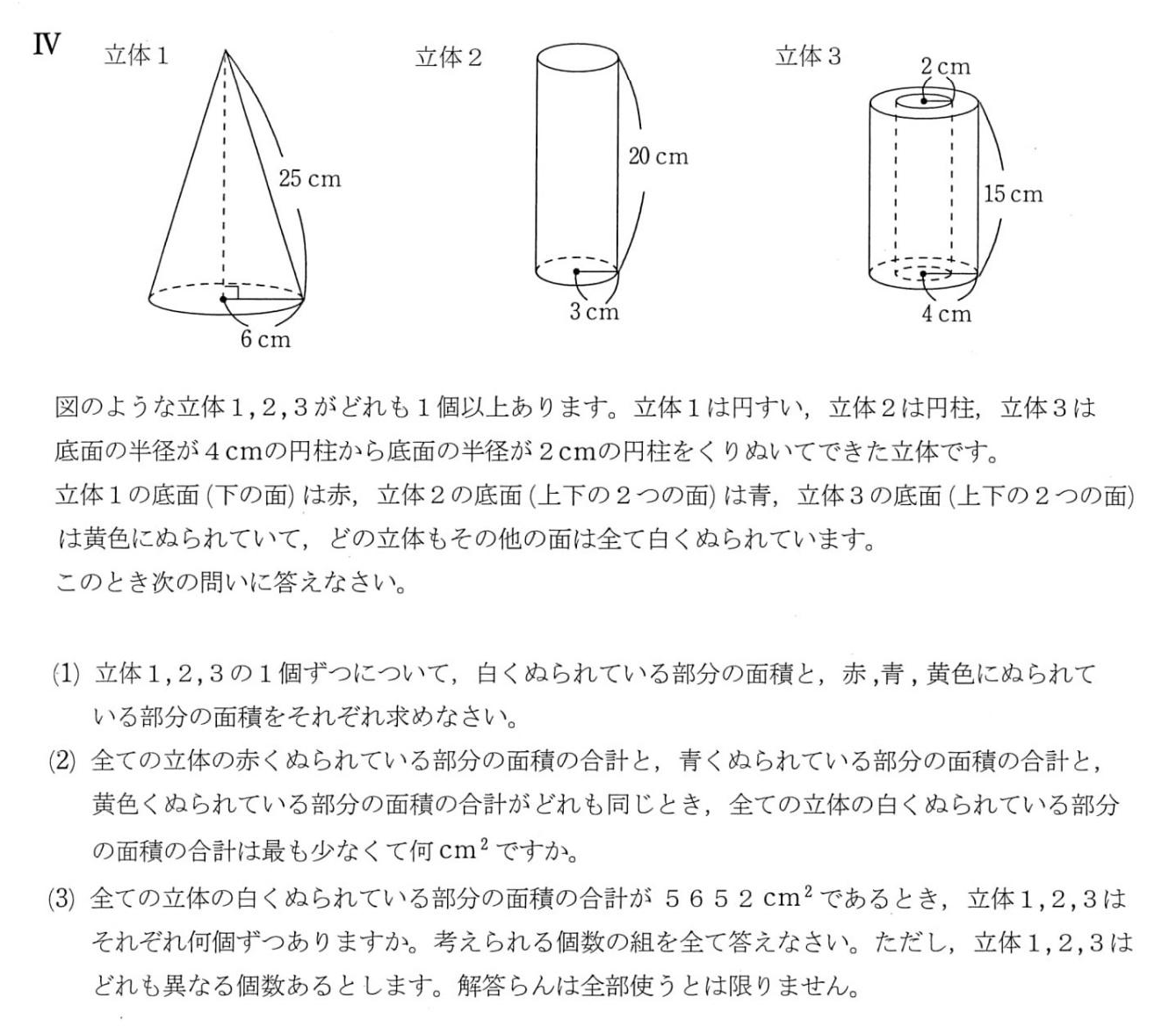
桜蔭中学の平成29年度のⅣを取り上げます。
〈考え方〉計算が煩雑になることは目に見えているが、シンプルにまとめることを目指す。
求めなければいけないものが多いので表にまとめます。
それぞれの面積を円周率=3.14で求めなければいけませんが表ではπのままにしておきます。
| 立体 | 色 | 面積(式) | 面積比 |
| 1 | 白 | 25×6×π=150×π | 25 |
| 赤 | 6×6×π=36×π | 6 | |
| 2 | 白 | 6×20×π=120×π | 20 |
| 青 | 3×3×π×2=18×π | 3 | |
| 3 | 白 | (4+8)×15×π=180×π | 30 |
| 黄 | (4+2)×π×(4-2)×2=24×π | 4 |
(1)表より
立体1 白…150×3.14=471(cm2)
赤…36×3.14=113.04(cm2)
立体2 白…120×3.14=376.8(cm2)
青…18×3.14=56.52(cm2)
立体3 白…180×3.14=565.2(cm2)
黄…24×3.14=75.36(cm2)
(2)面積比6:3:4の逆比が立体1,2,3の個数の比ですから
1/6:1/3:1/4=2:4:3
白の面積比を利用して
6×3.14×(25×2+20×4+30×3)
=1320×3。14
=4144.8(cm2)
(3)比を利用できるように面積の合計を3.14と6で割ります。
5652÷3.14÷6=300
立体1,2,3の個数をそれぞれx,y,z(個)とすると
25×x+20×y+30×z=300
両辺を5で割って
5×x+4×y+6×z=60
xが偶数であることと、x,y,zが全て異なることに留意して表を作ります。
(答)
| 完成した立体の個数 | ||||
| 立体1 | 2 | 2 | 4 | 4 |
| 立体2 | 8 | 11 | 1 | 7 |
| 立体3 | 3 | 1 | 6 | 2 |
※手順
1 立体1は偶数なので2、4…と順番に調べる。
2 立体1の個数を固定し立体2と立体3の組み合わせを見つける(この段階では同数でも良い)。1つ見つけたら立体2を3増やし立体2を2減らすという要領で他も見つける。
いかがでしたでしょうか。さすがにこの問題は何らかの形で「比」を使うのは必然でしょうが、なるべく煩雑さを避けられるように上手に「比」を利用しましょう。
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の1題比の文章題
難易度★☆☆☆☆
昨年はA中学校とB中学校の男子の人数の比は8:11、女子の人数の比は12:13、全体の人数の比は4:5でした。
今年はA中学校の男子が10%増え、女子が10人増えました。B中学校は男子が30%減り、女子が40人増えたので、2つの中学校の人数が等しくなりました。
(1)昨年のA中学校の男子と女子の人数の比を求めてください。
(2)今年のB中学校の男子と女子の人数をそれぞれ求めてください。
解答が表示されます