VOL.199規則性で間違えない（５）

この原稿を書いている夜は日本で３年ぶりに皆既月食が見られるそうです。

しかもこの日の月はスーパームーン！

スーパームーンとは満月が地球に最も近づく夜の月で、当然ながら最も大きく見えます。

最も大きな月が消えてなくなってしまうとは、何とも神秘的な夜ですね。

※皆既日食では実際は消えるのではなく全体が赤銅色に見えます。月が細くなる過程では欠けている部分は黒くて見えないのですが、全部隠れた瞬間、赤くなります。理科の問題で「なぜ赤くなるか答えなさい」というのもあります。解答例を最後につけておきます。

国内でのスーパームーンの皆既月食は１９９７年９月以来で、次回は１２年後だそうです。

おっと、そろそろ時間です。外に出て観測したいと思います。

さすがにターミナル駅の周辺なので周囲のビルが高く、月が見えません。少し場を変えてみましょう。

やはり、見えませんね。現在２０時なので、この時刻の満月は南東方向に見えるはずです。南東がひらけている場所に移動しましょう。

……やはり見えない。雲が厚いのか、空が真っ黒です。

このようにして、皆既日食の予定時刻は無情にも過ぎてしまったのでありました。

結局ネットで北海道や沖縄で観測されたものを見てお茶を濁しました。

皆さんは直接見ることができましたか？

もし見ていないなら、１２年後を楽しみに待ちましょう。次は晴れますように。

【規則性で間違えない】も５回目になりました。今回は「図形の規則性」について考えたいと思います。

「図形の規則性」はこのブログで言うところの「上級分野」かもしれません。

なぜかというと、「書き出し」がある程度制限されているからです。

数字ならば100個の書き出しは容易ですが、図形は必ずしもそうとは限りません。

前回の「今週の１題」は「５回目」を聞いていますが、全部描くのは容易ではないでしょう。

ではどうすればよいのかを、今回考えてみたいと思います。

Ⅰ．早い段階で規則性を見抜く

〈図１〉

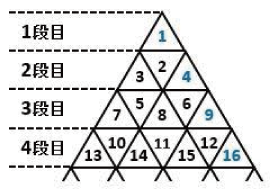
〈図１〉のような規則で三角形に番号を書き込む時、「1000」は何段目の左から何番目の三角形に書き込まれますか。ただし、「６」は３段目の左から４番目です。

ポイント：１番右が平方数になっています。

〈解説〉
３１×３１＜1000＜３２×３２
より３２段目
1000－31×31＝39
39－31＝8
8×2－1＝15（番目）

以上より（答）３２段目の左から１５番目

この問題はまず「１番右が平方数になっていること」を見抜きます。次いで、逆三角形がその上の段と辺を共有していることに気付けば、上記のように解くことが可能です。

確かめは、例えば４段目でやるとすると

４段目の数＝上の段の下側＋下の段の上側＝その段の平方－上の段の平方
　　　　　＝３＋４
　　　　　＝４×４－３×３
　　　　　＝７（個）
といった要領でよいでしょう。

Ⅱ．数字におきかえる

〈図２〉

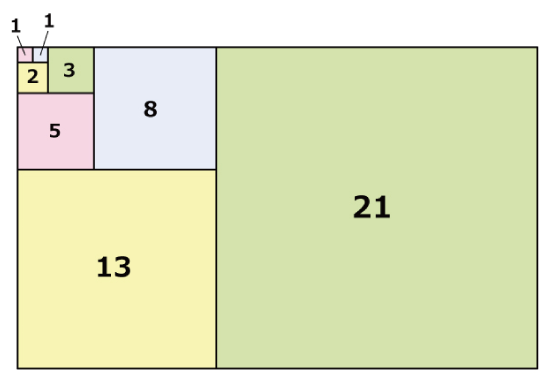
〈図２〉のように最初は１辺が１ｃｍの正方形２個に１辺が２の正方形をくっつけて長方形をつくる、ということを連続しておこないます。８個目の正方形の１辺の長さは２１ｃｍです。

では、１６個目の正方形の１辺の長さは何ｃｍですか。

ポイント：フィボナッチ数列になっています。

〈解説〉長方形に正方形をくっつけるのですが、長方形の長い辺と正方形の１辺の長さが等しくなっています。これを踏まえて表を作ります。

個数	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
短辺(cm)	1	2	3	5	8	13	21	34	55	89	144	233	377	610	987
長辺(cm)	2	3	5	8	13	21	34	55	89	144	233	377	610	987	1597

表より（答）９８７ｃｍ

まともに描くと途中から爆発的に大きくなってしまうので、正確な作図はまず無理です。

いかに早い段階で数字に置き換えるかが勝負となります。人によっては「フィボナッチ数列だから簡単だ」と思うかもしれませんが、設定が少し変われば結論も変わるので、知識だけだとやや危険です。

この問題のように「前の結果を利用するタイプ」は「表」の利用が効果的です。

今回は「図形の規則性」をとりあげました。やはりポイントは「図形⇔数量」ということになると思います。このあたりが「算数」ができるようになる最大のカギだと思うので、今後も色々な角度から検討していきたいと思います。

（解答例）赤い光は波長が長く散乱されにくいため、弱められながらも大気を通過することが可能である。この光が大気中で屈折され地球の影の中に入り込むことによって、月が赤く見える。