VOL.198規則性で間違えない(4)
新型コロナウイルスパンデミック関係の情報の中で、おやっと思うことがあります。
それは、死者数と重症者数の関係が見えないことです。
普通の感覚では、病院に行き、医師の診断で患者とみなされ、症状が重ければ入院等の処置がなされ、中にはその甲斐もなく亡くなる方もいる、という流れです。
ですから、死亡した方は重症者であった時期があるはずですが、そのようなことが読み取れる資料を目にする機会がなかなかありませんでした。
最近、本当の死亡者は1000人強なのではないか、という見解が、チラホラ見かけられるようになりました。
実はECMOnetというサイトがあり、ここにCOVID-19による人口呼吸器とECMO(人口心肺装置)の使用数や死亡者数が公表されていました。
このサイトは全国のおよそ8割をカバーしているので、おおよその数をつかむことができます。
数字は毎日変化するので、実質的な死亡者数をここでは計算しませんが、グラフの上に累計の死者数が書いてありますからECMOと人口呼吸器の分を足し、0.8で割ったものが実際の死亡者に近い数字と考えることができるでしょう。
それ以外にも、病院に行く間もなく亡くなった方もいるようなので、もう少し数は増えるかもしれませんが、現在、マスコミで報じられている数字は実体とかけ離れている可能性があります。
このように、情報を正しく評価するには、今算数で学んでいる資料の読み取りの力が不可欠です。
しっかり学びましょう。
さて、【規則性で間違えない】も4回目になりました。今回はあまり取り上げてこなかった「群数列」について書きたいと思います。
「群数列」とは、簡単にいうと「仕切りを入れてグループ分けすることによって規則性が見えてくる数列」のことです。
小学生はこの「仕切りを入れる」という作業は得意なようで、私が担当した生徒さんのほとんどが素早い反応で仕切りを入れていました。
小学生は直観力に長けていますから、ここは速いのですね。
分数列などは分母によりグループ分けができるのでほとんど間違えることはないでしょう。
では次の問題はどうでしょう。
1,2,2,3,4,4,5,6,6,7,8,8,9,10,10,11,12,12,13,14,14,15,16,16…
仕切りを入れるとしたらほとんどの受験生が
1,2,2|3,4,4|5,6,6|7,8,8|9,10,10|11,12,12|13,14,14|15,16,16|…
とやるでしょう。そして、「1番目から74番目までの和」をきかれたら、
74÷3=24あまり2
第25グループは(49,50)→50が欠けている。
グループごとの和は等差数列になっているから
(5+149)×25÷2-50=1875 …(答)
と解くことになります。当然、これは立派な解き方ですが、上の計算はかなり工夫しているので、ここまですんなりいかないかもしれません。
最初の仕切り方を
1,2|2,3,4|4,5,6|6,7,8|8,9,10|10,11,12|12,13,14|14,15,16|16…
とすれば「奇数列の和の3倍」ですから
(74+1)÷3=25
25×25×3=1875 …(答)
と暗算可能なレベルまで簡単になりました。
いくつか仕切り方が考えられる場合は、その後のこともイメージできると良いですね。
間違えないという観点から大切なことは、仕切り線を入れたら「グループ番号を振る」ことです。
実は今回一番言いたかったのはこれです。
早速やってみましょう。
Ⅰ.
①
1,2,2|②
3,4,4|③
5,6,6|④
7,8,8|⑤
9,10,10|⑥
11,12,12|⑦
13,14,14|⑧
15,16,16|…
Ⅱ.
①
1,2|②
2,3,4|③
4,5,6|④
6,7,8|⑤
8,9,10|⑥
10,11,12|⑦
12,13,14|⑧
14,15,16|⑨
16…
問題はここからで、グループ番号とグループ内の数字の関係をしっかりと見抜きます。
Ⅰ.・各グループは3個ずつ
・グループ番号の2倍が、2、3番目と等しくなっている。1番目は-1。
Ⅱ.・各グループは3個ずつ。ただし第1グループは最初に「0」があるとみなす(以下同様)。
・N番目のグループの真ん中の数は、N番目の奇数になっている。
・グループ内の数字は1ずつ大きくなっている。→真ん中は平均。
このような分析を行えば、群数列の問題は解けたも同然と言えるでしょう。
まとめます。
・群数列とピンときたら仕切り線を入れる。
・その際、直観に頼るのも良いが、普段の学習で別解に触れておくのも大切である。
・仕切りを入れたらグループ番号を振る。
・そして、グループ内の数字とグループ番号との関連を分析する。
・グループ番号が解法を思いつくきっかけになったり、確かめに使えたりと重宝するだろう。
今回はほんの一手間で正解率が上がる話をしました。是非実践してください。
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の1題規則性
難易度 ★★★★☆
正三角形の外側に小さな正三角形を付け足すことを1回の操作とし、それを何回か行うことを考えます。
ルールは
①他の三角形と接していない辺にだけ付け足す。
②1つの辺には、1辺の長さが3分の1の正三角形をはみ出したり重なったりしないよう 辺上に3個付け足す。
③別の三角形に付け足したものが重なった場合、それは1個と数える。
④1回の操作は、外側に対し全て付け足したところで終了する。その際、付け足した正三角形は全て合同である。
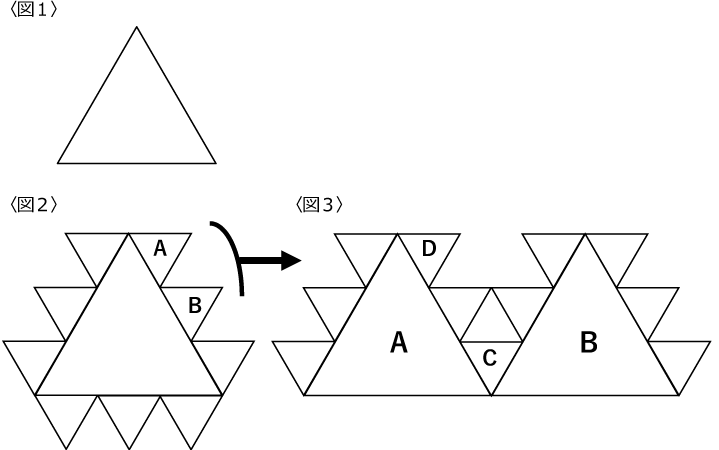
<図1>は最初の状態、<図2>は操作を1回行ったところで9個の正三角形が付け足されています。
<図3>は<図2>のA,B2つの正三角形を拡大したもので、2回目の操作を行ったところです。Cの正三角形は左右両方の正三角形に付け足されるものですが、1個と数えます。
(1)<図2>のAとBでは同時に付け足される三角形が、自身の3つの頂点に対してどのような位置にあるかという観点から(左右の違いは無いものとします)異なる性質の三角形とみる事ができます。
<図3>のAとC、BとCも異なる性質ですがAとDは同じです。
このような見方から付け足される正三角形は何種類かに分類できます。この操作を何回も行うとき、何種類に分類することが出来ますか。
(2)5回目の操作で付け足される正三角形は何個ですか。
*1回目の操作で付け足されるのは9個です。
解答が表示されます













