VOL.194【入試問題を解いての感想2021】 -(8)海陽-
太平洋上の雲の上部でかつてないほどの低温が観測されているというニュースを耳にしました。
マイナス111.2度が観測されたのは2018年末とのことです。
このたびこの原因が研究論文で明らかにされたので、ニュースになったようです。
雲は高度が上がるにつれて温度が下がります(理科で習います)。大気の最下層を対流圏といいますが、雲の勢力が強力であれば対流圏を突き抜け、成層圏に達しさらに冷やされます。
これを「オーバーシュート」というそうです。
先の最低温時には雲頂が高度20.5kmに到達し、マイナス111.2度という低温を記録したようです。
このような現象は近年頻繁に観測されるようになったそうですが、その原因はまだはっきりしていないようです。
「低温の雲は雷雨が強烈になりやすく、被害をもたらす危険性が高まる」と論文では警笛を鳴らしていますが、近年叫ばれている「気候変動」との関連については「解明の必要がある」と結んでいます。
このニュースに対しての私の感想は、「地球レベルで考えたら、1、2度は完全に誤差の範囲」というものです。地球の直径は約1.27万kmですが、それに対し20.5km上空に行くだけでマイナス111.2度になってしまうのですから、今温暖化してるといわれる僅か数度の上昇は、誤差の範囲かもしれないわけです。
さて、【入試問題を解いての感想2021】ですが、今回は海陽(特別給費生入試)を取りあげたいと思います。
比較的新しい学校ですが、抜群の進学実績で、あっという間にトップ校の仲間入りを果たしました。
入試の特徴は地元の名古屋以外でも受験が可能なことがあげられます。少なくとも東京会場は用意されているので、チャレンジャーを幅広く受け入れる姿勢が感じられます。
本ブログで扱うのは初めてなので、少しワクワクしますね!
それでは、内容をみていきます。
◎海陽(特別給費生入試)
1 小問集合
(1)倍数の総和の差をきいていますが、実質計算問題でした。ただし、三角数を利用するという工夫の余地がありました。
(2)「連続する整数の積の下何桁が0になるか」という問題とほぼ同じなのですが、「3の倍数の積」となっていたので、見抜けないと少し苦労したかもしれません。
(3)(あ)偶数を2の累乗に分割する問題でした。これは2進数の表記と同じです。
(い)2020を平方数に分割するのですが、650を見たとき、ピンときたかどうか。数的センスが問われた1問でした。
(4)タイルの敷き詰めの問題でした。複数の答が考えられますが1つ見つければ勝ちです。一番シンプルな考え方は、4×4の正方形を2種類で敷き詰め、それを鏡で映したものと1×4で完成させるというものだったと思います。
この手の問題は我々大人よりも子供達の方が得意ということも言えると思います。普段の学習では、上のような理詰めな考え方を学ぶと良いと思います。
2 約束記号→素因数分解後指数を全て1にしたものの積
(1)「まずはやってみましょう」という問題でした。
(2)ここからが本番ですが、これも別の言葉であらわせば「2の倍数」ということになります。
ここまでのところ、数の性質の問題が多いのと、別の言葉であらわすのが有効であることが目につきます。
(3)かなり本格的な記述問題です。わかっているけど、どうやって書けばよいか悩んでしまった受験生もいたことでしょう。ここは日頃の取り組み方で差がついた所だと思います。
3 逆ポーランド記法を理解する問題
(1)(2)「あなたは説明が理解できましたか?」という問題です。当然「理解できました。」と返さなければいけません。
(3)なかなか厳しい問題で、長々と説明していた問題文に戻って検証しないと、完答は難しかったかもしれません。この手の問題は後ろの設問がヒントになることもあるので、視野を広くして臨むようにしましょう。
4 正方形を2つに分割する問題→小さい方は10平方cm
(1)面積を求めるだけですが、2つの三角形に分割するという基本的な方針を定める必要があります。
(2)(3) (1)の「逆」ですね。「逆」になると答が複数になることがある典型的な例です。じつは、ここが(4)の誘導にもなっているので、しっかりとこの問題の「世界」に入り込んでいきましょう。
(4)主眼となる問題です。問題文の理解が最初の関門として立ちはだかります。冷静さが要求されたことでしょう。
前で複数考えられたものが1つに決まることがわかれば後は丁寧に調べれば良いのですが、最後の問題ということもあり、正答率は低めだったと思います。
全体的に、大人のテイストが漂う問題が並んでいるという印象を受けました。
私が本校の志望者を担当するならば、子供扱いは一切せず、一人前の人間として接するようにすると思います。
その上で、高級な知識に到達するまでしっかりと積み上げていくことが要求されるでしょう。
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の1題平面図形
難易度★★★★☆
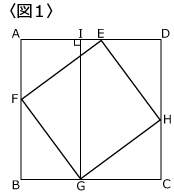
〈図1〉で、四角形ABCDと四角形EFGHはともに正方形です。
また、
EF=10cm、EI=2cmです。
(1)ADの長さを求めて下さい。
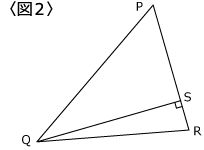
〈図2〉で∠PQR=45°、PS=10cm、SR=3cm です。
(2)三角形PQRの面積を求めて下さい。
※ヒント (1)の考え方を利用できる様な形を作って下さい。
解答が表示されます













