VOL.33志望校対策(6) 「麻布」
「男子御三家」の一角、日本を代表する名門校です。
入試も当然のことながらハイレベルなものになります。
対策を考えていきましょう。
「麻布」というとなんとなく「思考力」「発想力」を見る試験のような気がしますが、実際は「知識」「処理能力」を見る問題もバランス良く配置されていて、算数の総合的な力が問われる入試になっています。
後半はその場で書いて調べ、考えるタイプの問題が並んでいるので、60点満点のうち40点程度取ることを目標にするのが現実的だと考えられます。
もちろん、算数で稼ぐ必要がある場合は50点でも60点でも、多いに越したことはありません。
40点を取るための戦略ですが、「まずは30点取ること」が重要になります。
本校の場合、大問6題だとすれば、そのうちの3題が基本問題である可能性が高いです。
単純計算だとその3題を全問正解すれば30点キープです。
残りの30点のうち10点取れば目標達成です。
また、難しい問題であればあるほど誘導が丁寧なことが多く、肢問の前半は容易に答えられることが多いので、そこでの得点もある程度見込むことができます。
更に、本校の解答用紙は問題の下に四角に囲んだ空白があり、そこに途中の考え方・式等を書き、答を別の小さな□に書き込む方式なので、部分点も見込まれます。
以上から、基本問題を全問正解できれば、目標の40点に届く可能性がかなり高くなると思われます。
ただし、基本問題とは言え、麻布ですから、簡単というわけではありません。
幸い、頻出分野はある程度決まっています。
基本問題では、「計算」は置いておくとして、例年、「速さ」「数の性質」「平面図形」から出題されています。
これらの分野について、本校のレベルの「基本」をしっかりと身に着けておくのです。
分野ごとに見ていきましょう。
Ⅰ
速さ
「比」をうまく使えるかどうかで、難易度が変わります。「比」を使ったとしても計算が面倒になることが多いです。ある程度の量をこなし、入試問題特有のすっきりしない数値にも慣れておくと良いでしょう。
Ⅱ
数の性質
本校の特徴がよくでている分野です。初めて見るような問題が多いので、落ち着いて対応することが求められます。基本問題と言えども「その場で調べる」要素があったり、「発想力」が必要なこともあるので注意が必要です。ただ、後半で出題される本格的な問題の対策を行うことで、それらはカバーされるので、基本問題の対策としては、「知識の充実」をはかれば良いと思います。
Ⅲ
平面図形
「面積」に関係する問題が目につきます。「円」「移動」等とからめてあることも多く、やや上級といったところでしょうか。後ろの本格的な問題もそうなのですが、「正三角形」を組み合わせた形が非常に多いのも特徴です。「正六角形」もよく出ているので、形に慣れておきましょう。
以上、基本問題対策は完璧にしておいてください。
後半で出題される本格的な問題は「数の性質」「平面図形」に「規則性」や「場合の数」をからめたり、「割合」の問題に見えて実は「整数問題」だったりとなかなか奥が深いです。
全部を正解する必要はない受験生がほとんどだと思いますので、書いて調べて、自分なりの考え方を相手に伝えられれば十分だと思います。
この練習は集団では難しいですし、自分ひとりではほとんど意味がないでしょうから、個人的に指導者にみてもらうのが良いでしょう。
この部分だけで、10点ほどの上積みも可能でしょうから、合格への近道になる可能性があります。
ちなみに、本校の場合、他教科でも記述対策がポイントで、ここがうまくいけば逆転も可能な学校です。
今まで出てこなかった分野で、たまに出題される分野としては「立体図形」「割合・比」があります。
本校の受験生にとっては標準レベルであることが多く、基本がしっかりしていれば、特に問題はないでしょう。
過去問に関しては、少し多めにやっておくことをおすすめします。
なるべく解答用紙を実物大にしてから、そこに書き込む練習をします。
「答案をつくる」要素が大きい学校なので、その練習の機会を確保するために、過去問を多くやるのです。
本校の場合、独特な問題が多いので、他校では代役がきかないのです。
最後にまとめます。
- 基本的な問題とその場で考えるタイプの問題がバランスよく配置されている。日頃からこのバランスを崩さないような勉強を心掛ける。
- 基本問題は全問正解することを目標にする。頻出分野は決まっているので、その分野は徹底的に学習しておくこと。「麻布」が受験生に要求する「基本」のレベルは高いことに注意。
- その場で考えるタイプの問題は必ずしも完答しなくてもよい。途中までの考え方が採点者に伝わるような書き方を練習しておくこと。
- 苦手分野があるのは危険。全ての分野で標準以上の実力をつけておくことが望ましい。
- 過去問は多めにやっておく。本番サイズで「答案をつくる」ことを意識すること。指導者に添削してもらうことで、対策としての効果が上がる。
憧れの「麻布」ですから、そのハードルは高いです。攻略のポイントは基本からの積み上げです。
最後まで計画的に進めていきましょう。
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の練習問題麻布
難易度★★★★☆
(図1)の25個の点は最も近い点までの距離が全て等しくなっています。このように規則正しく並んだ25個の黒点のうち3点を結んで正三角形を作ります。
正三角形は120°回転すると元の形に重なりますが、このときの中心を「回転の中心」と呼ぶことにします。
面積が等しく「回転の中心」も同じである2つの正三角形を作り、一方を何度回転させればもう一方と重なるかを考えます。そして、このときの角度を「重なる角度」と呼ぶことにします。
例えば、(図2)の三角形ABCと三角形DEFは面積の等しい正三角形で回転の中心はともに点Gです。三角形ABCを時計まわりに60°回転すると2つの三角形は重なります。
このときの「重なる角度」は60°ということになります。回転の方向は時計まわりでも反時計まわりでもかまいませんが、「重なる角度」は60°以下のものだけを考えるものとします。
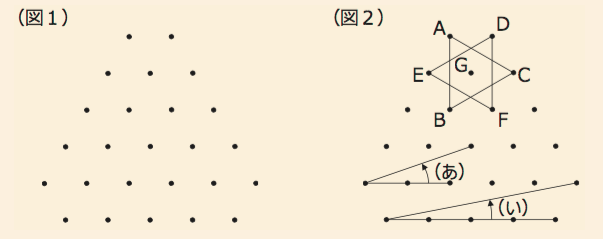
いま、三角形ABCの面積が3であるとき、以下の問に答えてください。
(1)
(図1)の25個の黒点のうち3点を結び正三角形を作るとき、全部で何個の正 三角形を作ることができますか。ただし、三角形の3辺が頂点以外の黒点を通らないものとします。
(2)
① (図2)の角(あ)と角(い)の和は何度ですか。
② (図1)の25個の黒点のうち3点を結び正三角形を作るとき、面積が7の正三角形同士の「重なる角度」と面積が21の正三角形同士の「重なる角度」の和は何度ですか。
解答が表示されます













