VOL.157【入試問題を解いての感想】 -(12)早稲田実業-
「慶應」を取り上げて「早稲田」を無視するわけにはいかないと思い、今回は本校を取り上げました。
早稲田系の中学校はいくつかありますが、古くから人気のある「早稲田実業」について書きたいと思います。
高校野球でも実績がある本校はまさに「文武両道」ですね。
算数の入試問題といえば一昔前は恐ろしいほどの難問を出すことで有名でしたが、最近はそれほどでもないように思います。
今年はどんな問題だったのでしょうか。
◎早稲田実業
1小問集合
(1)計算
「分数・小数混合の□の計算」という、難関校の計算問題でよくあるものでした。
ここで注意が必要だったのは「0.675」で、これは「 5 8 」ではなく「 27 40 」です。
引っかからないように注意してください。
(2)還元算
線分図を描いて、後ろから丁寧にたどっていけば正解できたでしょう。
学校側は最低限の基本ができているかどうかを見たかったんだと思います。
(3)道順
(1,1)と書いても良いのですが、計算で処理したかった問題です。
全体から通行止めを通るルートを引く「余事象」の考え方が使えます。
(4)立体の切断
最初の難関が来ました。
三角柱を2つに分けるわけですが、求める立体の方を直接求めるか、そうでない方を求め全体から引くかの2通りの解法が考えられます。
お勧めは直接求める方で、公式を適用すれば解決します。
2小問2題
(1)時計算
文字盤がない時計の問題でした。
このタイプは経験がないとかなり苦しいと思います。
「う:え」が求まれば解決することに気が付けば方針が立てやすかったのではないでしょうか。
ここでも少し差がついたことでしょう。
(2)規則性
分数の群数列でした。
群数列のポイントはグループナンバーを振ることと、その数字とグループ内を関連付けることです。
本問の場合、グループナンバーの2倍がそのグループの「分母+分子」になっていることと、グループナンバーの2乗がそのグループの末尾の数の「番目」になっていることを押さえておけば十分でした。
33人の進行グラフに歩数と歩幅を絡めた問題
歩幅のところが逆比になっているよくある問題です。
3人の速さの比を求めたあとは連比の問題ですから、特に問題なかったと思います。
この問題は絶対に落としてはいけなかったでしょう。
42種類の食塩水を水槽に注ぐ問題
食塩水を混ぜる問題に「仕事算」の要素が加わっています。
少し考えにくいのは水槽の容積等が決まらないからですが、こういった場合は自分で設定してあげることで解決します。
例えば容積を「144」とおけば、「てんびん」を何回か使って最後まで解き切ることができます。
数字がやや煩雑なので、あまり面倒な計算にならないように工夫したい問題でした。
55つの半円内部の三角形の相似をテーマにした問題
やや複雑な「平面図形」の問題でした。
(1)は基本~標準の問題だったと思いますが、(2)(3)は厳しかったかもしれません。
ただ、答を出す過程ではそれほど面倒なことにはならないので、図形が得意な受験生はここで差をつけることができたことでしょう。
「3:4:5」の直角三角形は常識にしておいた方が良く、「裏返しの相似」や「砂時計型の相似を作る」といったことにも慣れておきましょう。
ちなみに、本問は「相似の発見」がテーマですが、「相似であることの証明」まで求められているわけではありません。
直感的に相似を見抜ければよいので、時間を有効に使うことを優先するようにしてください。
※普段の学習ではなぜ相似なのかを学ぶことはとても大切なので、そのあたりの切り替えは意識するようにしてください。
受験者平均点しか公表されていないようなので、推測の域を出ませんが、合格者の平均点は7割程度だったと思われます。
この問題で7割以上取ることはそれなりに大変だとは思いますが、できるところを確実に正解すれば届く可能性が大です。
基本を大切にし、それをミックスしたような問題にも対応できるようにしておくような勉強法が本校の場合大切だと思います。
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の1題相似
難易度★★★☆☆
〈図1〉で直角三角形ABCと三角形BCDは辺BCを共有しています。
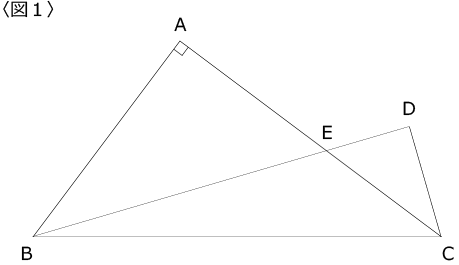
AB=15cm
BC=25cm
∠BCA=∠DCE
AE:EC=9:7
のとき、以下の問いに答えてください。
ただし、〈図2〉を用いてもかまいません。
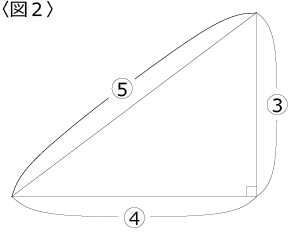
(1)∠BDCは何度ですか。求め方も書いてください。
(2)辺BDの長さは何cmですか。
解答が表示されます
(1)AC=25× 4 5 =20(cm)
AE=20× 9 9+7 = 45 4 (cm)
AE:AB= 45 4 :15=3:4
よって△ABCと△AEBは相似(2辺比夾角相等)。
△ABEと△DECにおいて、
∠AEB=∠DEC(対頂角は等しい)
∠ABE=∠ACB=∠DCE
よって△ABEと△DCEは相似(2角相等)
相似な図形の対応する角は等しいので、
∠BDC=∠BAC=90°…(答)(2)24cm













