VOL.143【入試問題を解いての感想】 -(1)灘 一日目-
毎年、学校の数の何倍かの入試問題が生まれます。
その全てに目を通すのはなかなか難しいですが、毎年楽しみにしている学校があります。
その筆頭が「灘中学」です。
私は小6の頃、神戸市の東灘区に住んでいたので、「灘中」のそばをよく通っていました。
塾も西宮北口からすぐのところにあったと記憶しています。
西宮北口は今も「塾銀座」と呼ばれているようです。
私が通っていた頃はユニークな色をした西宮球場が目立っていました。
今はどんな風景なのか、一度見てみたいですね。
灘中学のホームページを見ると、県別の志願者及び合格者の表が載っています。
地元の兵庫県は「市」ごとの内訳も載っているのですが、西宮市が神戸市を抑えて24名の合格者でトップになっています。
合格率も約45%(全体では約33%)と優秀です。
やはり、環境が人を育てるということなのでしょうか。
さて、今年の「灘中学」の入試問題ですが、昨年に比べ大幅に易化しました。
それでも面白い問題が多かったので、「一日目」と「二日目」を二回に分けて取り上げたいと思います。
◎灘 一日目
1 計算問題ですが、なかなか大変です。0.00125の処理をサッと行いたいですね。
2 消費税の問題。去年から10%になったので、出題は予想の範囲でしたが、皆さんはどうだったでしょうか。
3 速さと比の問題で平易でした。
4 本校特有の問題。過去問をしっかりやっていればいつも通りと感じたはずです。
5 パスカルの三角形からの出題。まだこんな性質があったのかと、数の奥深さを感じさせてくれた問題。
もしかしたら満点の障害になったかもしれない1題でした。
6 図形上の点の移動。変則の時計算とも言えますが、割とあっさり答がでます。
7 平面図形。平行四辺形につの出しして比をそろえれば終わり、という問題でした。
私ならこの問題を真っ先にやります。
8 6個全部をだそうとすると少し大変ですが、3個を求めた後は相似を使えば良い、という問題でした。
9 平面図形。いかにもという形をしていますが、合同に気づけば気持ちよく解決します。
10 回転体。まともにやると大変かもしれませんが、体積比を使うのが良さそうで、比較的きれいな数字で答がでます。
11 立体図形。本校で頻出である展開図から完成形をイメージできるかという問題です。
正四面体から切り出した形であることがわかれば、本校の受験生ならばどうにでもなったでしょう。
逆にこの問題ができなければ合格レベルには足りない可能性があるということだと思います。
良質な11題を味わうことができました。まさに至福の時間でした。
「図形」が易しめだったので、点数は取りやすかったという印象です。
実際合格者平均点が72点ですからミスは許されなかったでしょう。
本校の場合、対策が進んで合格者平均点が高くなってから灘中側の反撃が始まります。
今後どのような問題が生まれるか、来年以降も目が離せません。
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の1題平面図形
難易度★★★☆☆
〈図1〉のような正十二角形ABCDEFGHIJKLの内部を、まっすぐ進む点Pの道すじを考えます。
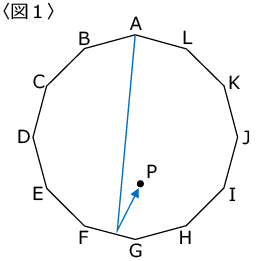
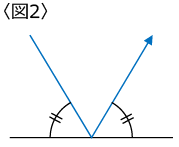
点Pは辺に到達すると、〈図2〉のようにはね返りますが、頂点に到達したときは、そこで止まります。
点Pは頂点Aから出発してはじめに辺FG上のどこかではね返りました。
(1)はじめに辺FG上ではね返った後、次に到達する辺として考えられるものをすべて答えてください。
(2)はじめに辺FG上のXではね返って、次に到達する辺でもう1回はね返って、頂点Dに到達しました。
FXはXGの何倍ですか。小数第3位を四捨五入して、小数で答えて下さい。
ただし、1辺が8cmの正六角形の面積は166.32cm2であるとします。
解答が表示されます













