VOL.140【ご質問フォーム】　－「筑波大学附属駒場中２０１１年大問１」－

2020/01/10

令和２年の一回目からは、来春６年生になる受験生を対象に１年間やっていきたいと思います。
どうぞよろしくお願いいたします。

さて、【ご質問フォーム】から２０１１年の筑波大学附属駒場中の大問１を取り上げて欲しいとの要望がありましたので、なるべくリアルにお伝えしたいと思います。

筑駒の問題について少し触れておくと（ＶＯＬ．３８参照のこと）、大問４問それぞれに肢問３問というスタイルが続いています。
（１）は易しめ、（２）が合否を分ける問題であることが多い気がします。
実際、（１）、（２）だけを正解すれば６０％強の得点が見込めるので「算数」だけでダメにすることはないと思われます。
もちろん正解は多ければ多いほど良いので、（１）、（２）を全問正解した上で残りの（３）も２～４問正解というのが理想的でしょう。
そこで大切になるのが解答順です。
早い段階で正解を確保すれば、理想に近づきます。
では、この２０１１年度の１はまっ先に解く問題でしょうか？
私なら、〔４〕（正三角形内部の線分のころがり）から解くでしょうが、いきなり解いても問題ないと思います。

〔２〕（条件を整理し調べる）は一番最後がおすすめで、後は得意な分野から解けば良いでしょう。
特に「図形」が得意な場合は、短時間で解ける可能性があるので、先に取り組むことをおすすめします。
さて、〔１〕に取り組むとなった場合、どのように解いていくかを書いていきます。

問題はこちらをクリック＞＞

まず、〈図１〉のような底面積がわかる図を描きます。

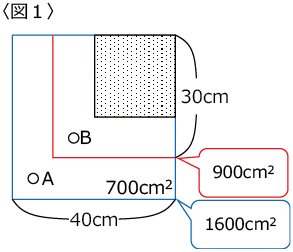
それを見ながら計算します。
底面積が７００ｃｍ^２の部分の水位を３０ｃｍ上げるのに２１０秒かかっているので、（１）は
７００×３０２１０＝１００（ｃｍ^３）　･･･（答）
と求められます。
次に「もし重りがなかったら」と考えます。
その場合、満水にするのにかかる時間は
４０×４０×４０１００＝６４０（秒）
なので、
６４０－５６０＝８０（秒）
早く水がたまったことがわかります。
重りの体積は８０秒間に給水される水の体積に等しいので
１００×８０＝８０００（ｃｍ^３）
また
８０００＝２０×２０×２０
なので重りの１辺の長さは
２０（ｃｍ）　･･･（答）

この時点で〈図１〉に面積が書き加えられ〈図２〉になりました。

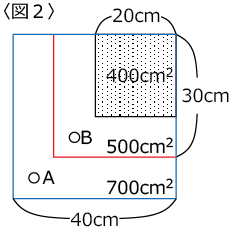
また（３）を解く方針ですが、問題文の図３のグラフに奥の部分の水位を書き入れ、その交点から求めることにします。
装置Ａの排水量は
７００×３０÷（５８０－１６０）＝５０（ｃｍ^３／秒）
装置Ａ＋装置Ｂの排水量は
１６００×１０÷１６０＝１００（ｃｍ^３／秒）
よって装置Ｂの排水量は
１００－５０＝５０（ｃｍ^３／秒）
とわかります。
〈図３〉は正面から見た図ですが、この図は描かなくても大丈夫でしょう。

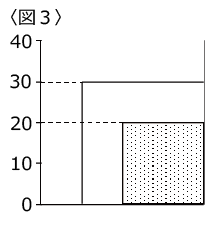
問題文の図１を代用します。
奥の水位が２０ｃｍになるのは
１６０＋９００×１０÷５０＝３４０（秒後）
で、０になるのは
３４０＋５００×２０÷５０＝５４０（秒後）
これを問題文の図３のグラフに書き入れると、〈図４〉のようになります。

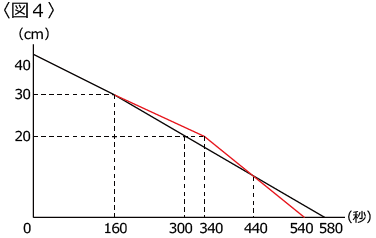
１６０＋（５８０－１６０）× １３＝３００（秒）
（３４０＋５４０）÷２＝４４０（秒後）…（答）
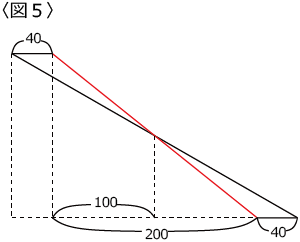
最後は〈図５〉のように砂時計型の相似を使い、フィニッシュです。