VOL.31志望校対策(4) 「フェリス女学院」
志望校対策の第4回は「フェリス女学院」です。
神奈川女子最難関校です。
問題も高級な考え方を題材にしたものが多く、どのような対策をしたかによって合否が分かれる可能性がある学校だと思います。
それでは、対策を考えていきましょう。
まず目につくのが図形を重視していることでしょう。
通常の「平面図形」「立体図形」だけでなく「図形の移動・図形上の点の移動」や「図形の場合の数」などの出題がみられます。
また「平面図形」「立体図形」ともに様々なバリエーションがみられ、毎年似たような問題が出るわけではないことがわかります。
以上から、「図形」が苦手では勝負にならないと言って良いと思います。
「立体図形」もある程度まではできるようにしておかなければ苦しいでしょう。
では「図形」をどの程度のレベルまでやっておけば良いのでしょうか。
私の感覚では「少し高級な考え方」までということになります。
基本的な考え方を組み合わせたり、掘り下げたりといったことはもちろんなのですが、考え方そのものが高級なものまで、理解しておいたほうが良いと思います。
具体的には、今年は「三角形の周の長さ・内接円の半径・面積の関係」、昨年は「立体の凹凸」がテーマとなっていました。
これらは数学をやった人間にとっては当たり前かもしれませんが、小学生には厳しかったと思われます。
また、数学で習う「円周角の定理」を知っていれば有利になったと思われる問題もありました。
こう書くと、数学の範囲までやっておいたほうが良いのか、という話になるのですが、それは違うと思います。
あくまで基本は算数なのであって、そこに少しだけ高級な考え方を上乗せするというイメージです。
ただ、その加減は非常にデリケートなので、指導者の下でやったほうが安全だと思います。
頻出分野の中で差がつきそうなものとしては「速さ」「数の性質」「場合の数」があります。
「速さ」は設定が複雑で計算が煩雑になることも多く、注意力が求められます。
「数の性質」はひらめきを要求されるような問題もみられるので、頭を柔らかくしておきましょう。
「場合の数」は難易度の設定が絶妙だと思います。
できれば正解する側にまわりたいですね。
そのために、計算で解ける問題は確実に計算で、書き出す必要がある場合は躊躇なく書き出せるように感覚を磨いておきましょう。
他の頻出分野に「割合・比」がありますが、ここは落とせないところになっています。
皆ができるところは確実に取り、差がつきそうなところでは離されないようについていくことが合格への道です。
本校の場合は、問題用紙に答を書くようになっており、途中式等も問題のところに書くように指示があります。
よって、難問に出くわしたときは部分点狙いという戦略も十分に考えられます。
過去問を解いたものを添削してもらえると良いですね。
以下にまとめます。
- 図形が苦手だと苦しい。少し高級な考え方まで身に着けておくと良い。
- 差がつきそうな分野は大体決まっている。その分野で、できる側にまわることを目標にする。
- 「割合・比」のような皆ができそうな分野は確実にとる。
- 処理能力・思考力のバランスが大切。
- 部分点狙いを視野に入れる。過去問を使い十分に練習しておくこと。
受験者平均点が例年5割前後であることを考えると、算数は失敗しなければ良いという考え方もあると思います。
どの学校にも言えますが、個々の実情に合った戦略で臨むことが重要です。
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の練習問題フェリス女子学院
難易度★★★☆☆
(図1)のように、角Bが90°の三角形ABCがあります。
直線DEは辺BCと、直線FGは辺ABとそれぞれ平行で、BGとDBの長さが等しくなっています。
また、角DFEは90°、ADの長さは26cm、三角形HGEの面積は162cm2です。
(図1)
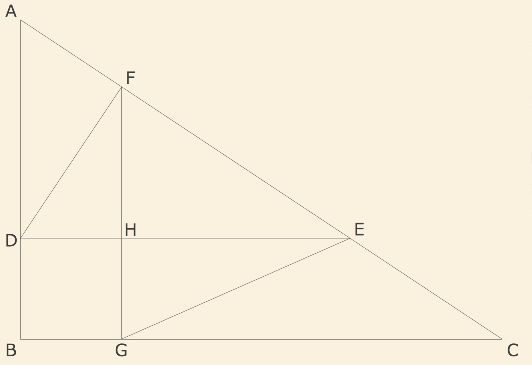
(1)
FHの長さを求めてください。
(2)
三角形ABCの面積を求めてください。
解答が表示されます













