VOL.111【場合の数攻略】 -場合分け-
入試問題は選抜の意味があります。
あまりにも簡単な問題だと差がつきませんから、難関校ではある程度難問が出題されるのは仕方ないことだと思います。
ところが、あまりにも難しいと誰もできないという現象が起こります。
これも差がつきませんから、選抜試験という意味ではあまりよろしくないわけです。
算数で差をつけようと狙っていた受験生にとっては、「簡単」と「度を超えて難しい」の両方が鬼門となります。
特に「難しい」場合、「できなかった」というマイナスの感情が残りますから、その後の出来に影響する可能性もあり、かなりの苦戦が強いられます。
このあたりは学校側に考慮してもらうしかありませんが、受験生側も四教科まんべんなく実力をつけておく必要はあるでしょう。
特に試験当日は反省してはいけません。
終わったことは忘れ、目の前の問題に集中するようにしましょう。
「場合の数」は難問が出題されやすい分野です。
なぜ難しくなるのかで分類してみます。
①数え上げれば良いがその数が多い、又は見落としやすいものがある
②数えるにしては数が多すぎるし、普通の計算ではうまくいかない
③条件が複雑でそもそも数えることが困難
他にもいろいろあるでしょうが、いずれにせよ単純に数えることを封じられたときに「難問」と化すように思います。
そこで今回のテーマですが、きちんとした数え上げを実現するための武器となる「場合分け」をやりたいと思います。
計算で解くにしても「場合分け」が必要なケースは多いです。
前回取り上げた「フィボナッチ数列」を使って解く問題の典型的なものに「階段」があることは常識になっていると思いますが、次のような出題のされ方の場合はどのようにして解くでしょうか。
<問題>
7段の階段があり、1番下から7段目まで上ることを考えます。
1段ずつ上るか、1つ飛ばしで上るかの2通りの上り方があるとき、以下の問いに答えてください。
(1)1つ飛ばしを1回行うとき、何通りの上り方がありますか。
(2)1つ飛ばしを2回行うとき、何通りの上り方がありますか。
(3)全部で何通りの上り方がありますか。
<答>(1)6通り (2)10通り (3)21通り
<解説>
フィボナッチ数列を利用する解法ならば(3)は
1+2=3
2+3=5
3+5=8
5+8=13
8+13=21(通り)
と求められます。
しかし、(1)(2)は別の考え方が必要です。
(1)一つ飛ばし1個と1段ずつ5個の並べ方とみれば6通りとすぐに見抜けます。
(2)一つ飛ばし2個と1段ずつ3個の並べ方は5個の中から2個を選ぶ組み合わせなので
5×4 2×1 =10(通り)
(3)(1)(2)以外は
i)一つ飛ばし3回→3個と1個の並べ方なので4通り
ii)一つ飛ばし0回→1通り
よって全部で
6+10+4+1=21(通り)
以上見てきたように「階段」は「場合分け」をして解くのも有力だったことがわかります。
上の問題の場合は「場合分け」することによって「組み合わせ」の公式が使えるようになりました。
このように、「場合分け」することによって公式が使えるようになることは「色ぬり」などでもよくあるので、いつも意識するようにしてください。
次に「場合分け」によって数えやすくなるケースを見てみます。
<問題>
〈図1〉のように3×3のマスがあります。
このうち2つのマスを黒く塗るとすると、その塗り方は何通りありますか。
ただし回転して重なるものは1通りとして数えます。

<答>10通り
<解説>
この問題の場合何も考えずに書き出しても正解できるかもしれませんが、いかにも危険です。
効果的な場合分けを考えてみます。
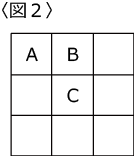
〈図2〉のように正方形の頂点にあたるような位置にある4つのマスをA、辺にあたる4つのマスをB、真ん中をCとします。
2つ選んで黒く塗るのですが組み合わせとして考えられるものは
(A,A)(A,B)(A,C)(B,B)(B,C)
なのでそれぞれについてみていきます。
①(A,A)
同一辺上か対角かで…2通り
②(A,B)
Aを左上に固定すればBは4か所どこでも良いので…4通り
③(A,C)
どのAを選んでも回転すると重なるので…1通り
④(B,B)
斜めか向かい合わせかで…2通り
⑤(B,C)
③と同様に…1通り
以上より和の法則を使って
2+4+1+2+1=10(通り) …(答)
この問題の場合は答が「10通り」と小さい値だったので、場合分けは必須ではありませんでした。
しかし、もう少し増えてくると何の方針も立てずに数えることはおすすめできません。
抜けやダブりの心配もしなければなりませんし、そもそも終わりが見えない数え上げは危険すぎます。
上の問題は3×3でしたが4×4だとそこそこ難しい問題になります。
答を1番下に書いておくので、自信のある人はやってみてください。
方針が立ちにくいもの、ゴールが見えにくいものは、「場合分け」をして上手くいかないかどうかを検討してみてください。
そうやって手を動かしているうちに答にたどり着くということも多いと思います。
<練習問題の答>32通り
具体的な算数の問題に関するご質問など、お子様の中学受験に関してお困りの点がございましたら、こちらのフォームからご質問を承ります。
お寄せいただいたご質問へは当ブログ上にてご回答させていただきます。
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の1題場合の数
難易度★★★★★
〈図1〉のように4種類の形をしたタイルがそれぞれ何枚かあり、これらを使って長方形(正方形)の枠の中をすき間無くはりつけることを考えます。
ただし、タイルは裏返すことができません。
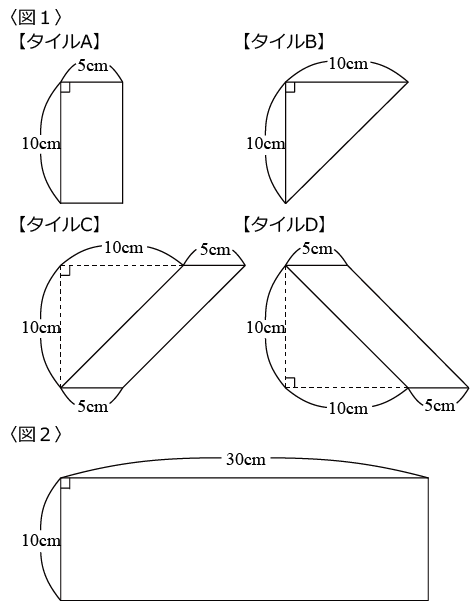
(1)〈図2〉のようにたて10cm、よこ30cmの長方形の枠の中をすき間無くはりつける方法は何通りありますか。
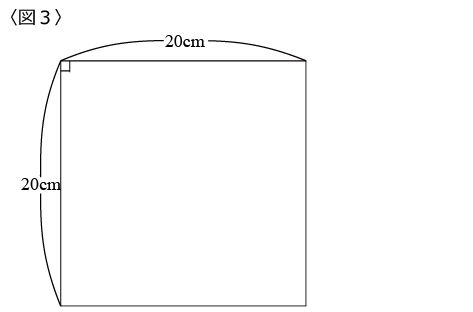
(2)〈図3〉のように1辺が20cmの正方形の枠の中をすき間無くはりつける方法は何通りありますか。
解答が表示されます













