VOL.109【場合の数攻略】 -苦手からの脱出-
塾の教材や市販の問題集には様々なものがあります。
問題に対する解法もどれも同じということは稀で、複数の考え方が存在することが多いです。
それでも、複数の解法の中での優劣のようなものは存在します。
各教材の著者は、見るものにとって最善であろうものを選んで採用しているはずです。
その教材が良いか悪いかの判断基準のひとつに、「解法の選択が、学んでいる受験生にフィットしているかどうか」があります。
ただ、これが個々の受験生にドンピシャリということはまずありません。
なぜならば、現在の力量や性格、今までに学んできた内容等が受験生一人ひとりで異なるからです。
応用問題に取り組む際、複数の解法があることについて、私が授業で心掛けていることは主に以下の3つです。
①生徒の考え方はとりあえず尊重する
→ 途中で挫折したとしてもその先に解決策があったりする
②今までやってきたことを活かす
③現時点で最善と思われる解法を明確にする
①についてですが、方向が明らかに違っている場合は別ですが、かなりの確率で正解までたどり着きます。
私にとっても新たな発見があったりするので、小学生の自由な発想は尊重したいです。
②はかなり重要です。
解法の基本をしっかり学習していれば、それらを組み合わせたり、少し深めたりすることで大抵の問題は解けるはずです。
ですから勉強量を少なくしたければ、厳選された解法をしっかりと頭に入れ、後はそれらを運用する練習をすればよいのです。
私がお手伝いできるのは、あらかじめ頭に入れておくべき範囲とその場で考えるべき範囲の線引きです。
そして、応用問題と言えども、根本的な部分では基本問題に帰着することがほとんどであり、その基本問題は大抵の場合学習済であるので、それを活かせれば応用問題も解けるということです。
何でもそうなのですが、結論は明確にしないといけません。
そうしないと、学習の姿勢がブレてしまう可能性もありますし、何をどうしたら良いかが分かりにくくなってしまいます。
そして、この「結論」を選ぶところに個性が出るわけです。
もしかしたらここに講師の力量が反映されるのかもしれません。
前置きが長くなってしましましたが、今回から【場合の数攻略】と題して、私の考え方を披露したいと思います。
なぜ冒頭であんな話をしたかというと、「場合の数」の分野が最も解法のバラつきが多いと感じているからです。
解法のバラつきが多いということは、受験生にとってフィットする確率が下がることを意味するので、「独学が難しい」という結論になります。
確かに「場合の数」が得意という生徒にあまり会ったことがありません。
受験の戦略上の「場合の数」の位置付けですが、確実な得点源としての計算は立ちにくいので、出来ればライバルに差をつけることができるボーナスのように捉えておくのが無難だと思います。
ですから、まずは「苦手からの脱出」を目標に掲げたいと思います。
どちらかというと「苦手」側の人間は数多く見てきていますが、そこにはある共通点があります。それは「バランスが悪い」ということです。
「算数」ができるようになるために真っ先に気を付けるべきことは「バランスを整える」ことだと思います。
以下にいくつか例をあげます。
・スピードと正確性
・数量と図形
・筆算と暗算
どれもどちらかに偏ると安定性が失われると考えられます。
そして、「場合の数」でもっとも影響しそうなのが、「書き出し」と「計算」のバランスです。
「苦手」な人というのはワンパターンであることが多く、特に「計算」でしか解けないタイプだと、なんでもかんでも「順列」か「組み合わせ」で解こうとします。
また、「何でも書き出し派」は1000通りあるものも書き出そうとして自滅したりします。
ここからは「何でも計算派」をⒶタイプ、「何でも書き出し派」をⒷタイプとして話を進めます。
例えば次のような問題をⒶタイプはどのように解くかを見ていきます。
<問題> A、B、C、D、E、Fの6人を3人と3人に分ける方法は何通りありますか。
《Ⓐタイプの解法》
6人の中から3人を選ぶ組み合わせだから
6×5×4 3×2×1 =20(通り) …×
《バランス派の解法》
ABC‐DEFとDEF‐ABCは同じなので(書いて確かめた)「6人の中から3人を選ぶ組み合わせ」だとダブってしまう。
よって
6×5×4 3×2×1 ÷2=10(通り) …〇
Ⓑタイプの正解率は答が何通りかによるので、この問題は正解できる可能性が高いでしょう。
どう描くかで手間が変わってくるので、そこは検討の余地があります。
基本的にはツラツラ描くよりも樹形図がお勧めです。
この問題も計算で解くやり方を自分のものにしておくことは可能です。
Aについて、残りの2人が決まれば全体も決まるので「5人の中から2人を選ぶ組み合わせ」となり
5×4 2×1 =10(通り)
と解くことができます。この考え方を理解しておけば
「8人のトーナメント戦の対戦の組み合わせは何通りあるか」
といった問題を解くことができます。
《解答》
8人を2人×4に分け、その4組を2組×2に分ける。
(7×5×3×1)×(3×1)=315(通り)…(答)
少し話が横道に逸れてしまいました。
「Ⓐタイプ」「Ⓑタイプ」それぞれの長所・短所を見ていき、最後にどのようなバランスが望ましいかを考えてみたいと思います。
【Ⓐタイプ】
| 長所 |
・「順列」または「組み合わせ」は公式を利用してサッと解ける。 ・時間をあまりかけないので、仮に不正解だったとしてもさほど痛くない。 ・深い勉強をしていれば、かなりの難問も簡単に正解できる可能性がある。 |
|---|---|
| 短所 |
・実際の入試問題では単純な問題はあまりないので、解ける問題がほとんどないということもあり得る。 ・考えるということをあまりしない傾向があるので、普段の勉強で「思考力」が鍛えられない。 |
【Ⓑタイプ】
| 長所 |
・「算数」の基本に「書く」ことがあるので、その意味では理にかなっている。 ・難関校では「書き出し」によって答を出す問題が好まれる傾向にある。 ・普段から手を動かすことによって「思考力」が鍛えられる可能性がある。 |
|---|---|
| 短所 |
・正解に至るまでにある程度の時間がかかる。 ・数が大きくなるにつれ正解率が下がっていき、一定以上の場合は破綻する。 |
それぞれ一長一短があるので、できれば良いとこ取りをしたいですね。
実は私は「Ⓐタイプ」寄りです。
できれば全部計算で解きたいのです。
例えば「道順」の「1、1」と書く解法は有名ですが、あれは計算でも求めることができます。
可能な限り深いところまで学習しておき、「計算」で解ける問題は基本的には「計算」で解き、そうでないものは「書き出す」というのが私のバランスです。
一般的な受験生の場合は「深さ」に限度がありますから、明らかに「順列・組み合わせ」という問題以外はまずは「書き出す」ことをお勧めします。
そして最後まで「書き出す」のではなく、「形」や「規則性」が見抜けた時点で「計算」に移行するのです。
まずは「書き出し」、隙あらば「計算」というバランスを身に着けた時、「場合の数」に対する「苦手意識」は払拭されることでしょう。
具体的な算数の問題に関するご質問など、お子様の中学受験に関してお困りの点がございましたら、こちらのフォームからご質問を承ります。
お寄せいただいたご質問へは当ブログ上にてご回答させていただきます。
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の1題道順
難易度★★★★☆
〈図1〉はA、B、Cを含む25個の玉を40本の棒でつないだ様子を表しています。
点PがAから棒を通って他の玉に移動するとき、何通りの経路があるか考えます。
また、Aについては条件につき考慮しないものとします。
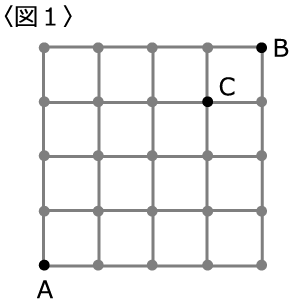
(1)点PがAからC、CからAと最短の経路で往復します。
その際、どの玉も棒も1度しか通らないとすると、何通りの経路がありますか。
(2)点PがAからB,BからAと最短の経路で往復します。
その際、どの棒も1度しか通らず、行きと帰りで1つだけ同じ玉を通るとすると、何通りの経路がありますか。
解答が表示されます













