VOL.107【図形に強くなる】 -立体の公式-
今回は「立体図形の公式」をまとめてみたいと思います。
「公式」は本の裏表紙に当たり前のように書かれているので、軽視される傾向にある気がします。
ですが、「なぜそうなるのか」を突き詰めていくと結構面白く、「考える力」の養成にもなるので、今回取り上げました。
また、「立体図形の公式」を扱うためには「平面図形の公式」が全て頭に入っている必要があります。
忘れていないかどうか各自確認してみてください。
実は扱える「立体図形」は「柱体」と「すい体」だけなので、それぞれについて公式を紹介し、なぜそれで求められるか等を考えてみます。
①柱体
(表面積)
表面積=底面積×2+側面積=底面積×2+底面の周×高さ
とくに
円柱の表面積=底面の半径×底面の半径×円周率×2+底面の直径×円周率×高さ=(底面の半径+高さ)×底面の直径×円周率 …(A)
「柱体」は「ふた」と「底」が合同ですから、底面積×2は納得でしょう。
また、側面を展開すると長方形になりますから、その面積は「長方形」の「たて×よこ」で求められます。
「たて」はその「柱体」の「高さ」に等しく、「よこ」は「底面の周」に等しいので、上のような式になります。
円柱の表面積は計算をすっきりさせるために(A)のように「□×円周率」の形にしておくと良いと思います。
ここで出来上がった(A)の意味について考えてみましょう。
「底面の直径×円周率」は円周になるので、式の意味は「円周×底面の半径」と「円周×高さ」の和ということになります。
「円周×高さ」が「側面積」を意味することは明らかですが、「円周×底面の半径」の意味するものは何でしょうか。
VOL.104の「今週の1題」の冒頭に答がありまして、結論は「円」2個分で、納得のいく式ということになりました。
(体積)
体積=底面積×高さ
ここで、そもそも「体積」とは何か考えてみます。
辞書を引くと「立体が占める空間の大きさ」のように書いてありますが、「立体の大きさ」と捕らえておけば問題はないでしょう。
実はこの「体積」の値というものは「比」です。
たとえば「100cm3」というのは
「1辺が1cmの立方体の100倍の大きさ、比で言えば「100:1」
ということです。
そうすると「底面積」は「1辺が1cmの正方形の何倍か」という意味であり、高さは「1cmの何倍か」ということをやっているわけです。
そして「1cm」というのは元々
「地球の北極から赤道までの子午線の長さの1000万分の1(1m)の100分の1」
ですから、知らず知らすのうちに地球とサイズ比べをしていたのですね。
※現在の「1mの定義」は「1秒の299,792,458 分の1の時間に光が真空中を伝わる距離」となっています。
②角すい
(表面積)
表面積=底面積+側面積=底面の多角形の面積+側面の全ての三角形の面積
これを見ると、求めることができるケースがかなり限定されることがわかります。
底面は三角形か四角形であることが普通で、さらに三角形のときは直方体から切り出すようなケースがほとんどでしょう。
切り出したケースでは切り口の面積が厄介です。
大抵の場合一筋縄ではいきません。
最も難しいと思われるレベルがVOL.92の「今週の1題」にありますので参考にして下さい。
(体積)
体積=底面積×高さ× 1 3
公式自体は特に難しいことはありませんが、なぜ「 1 3 倍」するのかを考えたことのある人はあまりいないでしょう。
小学生でも「 1 3 倍」になりそうなことが理解できる形があるので紹介します。
1辺が6cmの立方体を考えます。
この立方体の中心と各頂点を直線で結ぶと6個の合同な四角すいに分割されます。
この四角すい1個の体積は
6×6×6÷6=36(cm3)
です。
またこの四角すいと底面積と高さが等しい四角柱の体積は
6×6×6÷2=108(cm3)
ですから、確かに 1 3 倍になっていますね。
③円すい
(側面の展開図のおうぎ形の中心角)
中心角=360°× 底面の半径 母線
(側面積)
側面積=母線×底面の半径×円周率
(表面積)
表面積=底面積+側面積=底面の半径×底面の半径×円周率+母線×底面の半径×円周率=(母線+底面の半径)×底面の半径×円周率 …(B)
(体積)
体積=底面積×高さ× 1 3 =底面の半径×底面の半径×円周率×高さ× 1 3
円すいは公式の数が多いです。
いっぺんに紹介しましたが大丈夫でしたか?
まず、「中心角」の公式ですが、これは「割合」や「速さ」の公式と同じく、「母線」「半径」「中心角」の3つのうち2つがわかれば残り1つは求められることを示しています。
「側面積」の公式はかなり重要で、「おうぎ形」の面積の公式である
「半径(母線)×半径(母線)×円周率× 中心角 360° 」
は極力使わないようにしてください。
「表面積」に関しては上の最終形のようにしておくのが良いように思います。
今回特に注目したいのは「円柱の表面積」である(A)と(B)の関係です。
式からも明らかなように(A)は(B)の2倍になっています。
まとめると〈図1〉のようになります。
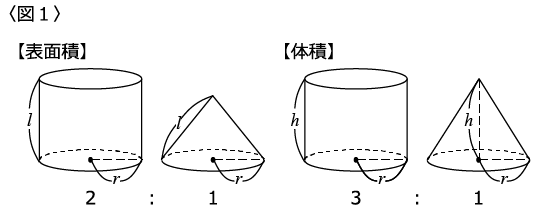
円柱と円すいがあり、表面積に関しては
「底面の半径が等しく、円柱の高さと円すいの母線の長さが等しければ、その表面積の比は2:1になる」
ということです。
また、体積に関しては
「底面の半径が等しく、高さも等しければ、その体積の比は3:1になる」
というおなじみの結論です。
「立体図形の代表的な公式」を紹介しましたが、新たな発見はあったでしょうか。
これを機会に基本の確認をしてもらえれば幸いです。
具体的な算数の問題に関するご質問など、お子様の中学受験に関してお困りの点がございましたら、こちらのフォームからご質問を承ります。
お寄せいただいたご質問へは当ブログ上にてご回答させていただきます。
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の1題立体図形の移動
難易度★★★☆☆
〈図1〉のように1辺が12cmで、3つの頂点をa、b、cとする正三角形の板があります。

また、〈図2〉のように底面の半径が、高さが8cm、母線が10cmの円すいが3個あります。
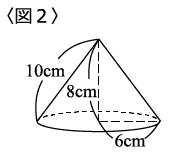
今、3個の円すいの中心がそれぞれa、b、cと重なるように、板の上にのせ、立体Pを作りました。(〈図3〉)
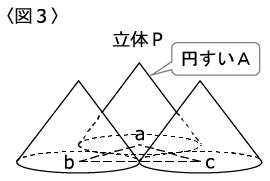
ここで特に底面の中心がaである円すいを円すいAとすることにします。
以下の2回の移動を3つの円すいの底面が同一平面上にあるようにして行いました。
① 点aを中心として時計回りに120°回転
② ①の移動後に点bを中心として円すいAだけを反時計回りに180°回転
①と②の移動によって、立体Pと円すいAが通った範囲すべてで構成される立体をQとします。
円周率を3.14、板の厚みを考えないものとして、以下の問に答えてください。
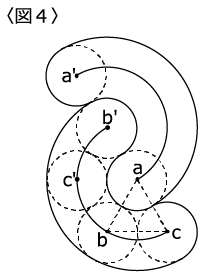
(1)立体Qを真上(円すいの底面が通った面に対して垂直な方向)から見るとどのようになりますか。
〈図4〉にかき加えてください。
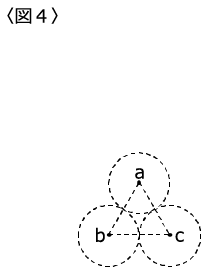
(2)立体Qの体積と表面積をそれぞれ求めてください。
解答が表示されます
(2)体積4220.16cm3、表面積3014.4cm2













