VOL.94【計算名人への道】インド式計算（2）　－２桁×２桁の暗算－

前回、「インド式計算」の「１０の位の数字が同じで、１の位の数字の和が１０になる場合」を紹介しましたが、その後の「今週の１題」でも明らかなように、「１０の位以上の数字が同じ」でも、あの方法が使えます。
理由は面積図から明らかだと思いますが、そういったことに自分で気づけると良いですね。
※具体例を挙げておきます。

１２３×１２７を求めます。
①１２×（１２+１）＝１５６
②３×７＝２１
③よって（答）１５６２１

さて、今回も「インド式計算」の一つを紹介したいと思います。

使える範囲が広い「２桁×２桁の筆算」です。

これのやり方については、ちょっと調べただけで３通りほどありましたので、「筆算」が最もやりやすそうなものを紹介したいと思います。

では、５６×７９を例にやり方を説明します。

もう少し例を挙げておきます。

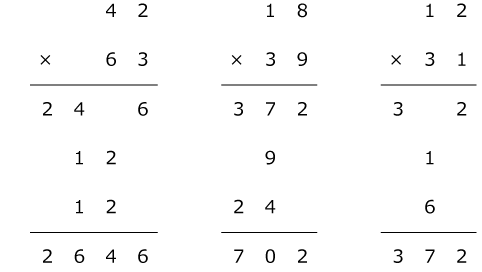
どうでしょうか。
「日本式」とあまり変わりなかったですか。

このやり方には明らかなメリットがあります。
「日本式」の場合、筆算の過程で位が上がったときの数字を小さく書いてメモすることがありますが、それをやらなくて済む、これが大きいのです。

特に小学生の場合まだ上手に字を書けていないこともあり、あの小さな数字のメモが原因で計算ミスをすることが多々あります。
その心配が無くなるだけでも「インド式」を取り入れる価値はあると思います。

そして、今回最も言いたかったことは、「２桁×２桁の掛け算の暗算」にチャレンジしようということです。

計算ができる・できないを分けるのは暗算の力だと思っています。
「間違いを防ぐために暗算は避ける」ということとは別問題です。
日頃から暗算力を高めるためのトレーニングを行っていれば、計算力不足に悩まされる心配はなくなります。

そこでおすすめなのが、「２桁×２桁の掛け算の暗算」を「インド式」で行うというものです。

５６×７９を例に私のやり方を説明します。
まず先に
５×９＋６×７＝８７
をやってしまいます。
この８７をしっかりと頭にやきつけます。
次いで、
６×９＝５４
より、一の位は４で確定ですから４は書きます。
次いで十の位は先ほど記憶しておいた７と５を足せば良いので
５＋７＝１２
より、十の位は２、
８＋１＝９
ですから、最後に
５×７＋９＝４４
をやり、すでに書いてある２４の前に４４を書いて
５６×７９＝４４２４
が完成します。

こうやって説明すると面倒なようですが、慣れれば難しくないので、パズルを解くような感覚で楽しんでもらえればと思います。
自分なりのやり方でかまわないので、色々と試してみてください。暗算力の向上に役立ちますよ。

具体的な算数の問題に関するご質問など、お子様の中学受験に関してお困りの点がございましたら、こちらのフォームからご質問を承ります。
お寄せいただいたご質問へは当ブログ上にてご回答させていただきます。