VOL.93【計算名人への道】インド式計算（１）　－２桁×２桁の暗算－

皆さん、こんにちは。

このブログも３シーズン目に突入することとなりました。
ここまで来ることができたのはご覧になってくださった方々のおかげです。

これからも受験生の助けになるような情報を発信していきたいと思います。
よろしくお願い致します。

さて、現６年生はこれから受験が佳境に入るわけですが、新６年生も１年後には受験本番直前なんですね。

まだまだ先のことと感じられるかもしれませんが、やらなければいけないことが山のようにあるのも確かです。
優先順位を明確にして計画的に取り組んでいってもらいたいと思います。

「算数」に関してはどこまでいっても「計算」が大切であり、できなければネックになってしまうということを感じます。

じつは「計算」は大学受験でも大切なので、今からしっかりと鍛えておきたいですね。

そこで、しばらくの間「計算名人への道」と題して、計算が強くなりそうなお話をしていきたいと思います。

第一回は「インド式計算」についてです。

「インド式計算」はかなり前から脚光を浴びていたようですが、私は特に必要性を感じなかったので、自分の指導の中に取り入れるということはありませんでした。

しかし、「日本式」よりも楽なことが多く、色々とメリットがあることも確かです。

「インド式計算」は数々の本が出版されており、ネットでも色々書かれています。
私は、何をもって「インド式」かということを完全に理解しているわけではないのですが、受験算数での活かし方のようなものはわかってきたので、それを紹介したいと思います。

「インド式計算」の特徴は

①パターンが細分化されている

②数学の考え方がベースになっている
【例】（１０ａ＋ｂ）（１０ｃ＋ｄ）＝１００ａｃ＋１０（ａｄ＋ｂｃ）＋ｂｄ

といったところでしょうか。

中学受験で絶対的に有用と思われるのが２桁×２桁の掛け算です。
その中でも特ににマスターしておいた方が良いものを今回紹介したいと思います。
それはズバリ
「１０の位の数字が同じで、１の位の数字の和が１０になる場合」
です。

では具体例を挙げて説明しましょう。

８７×８３
のような計算は九九の延長でできてしまいます。
８×（８＋１）＝７２
と
７×３＝２１
この２つをくっつけて７２２１が答です。

３４×３６
なら
３×（３＋１）＝１２
４×６＝２４
より、１２２４が答です。

ほとんど時間がかからないですね。
当然筆算する必要はありません。
ぜひマスターしてください。

なぜこうなるかを考えてみます。
小学生の場合、面積図が理解しやすいでしょう。
上の３４×３６を例にして説明します。

３４×３６は〈図１〉の面積なので、（ア）～（エ）の和を求めます。

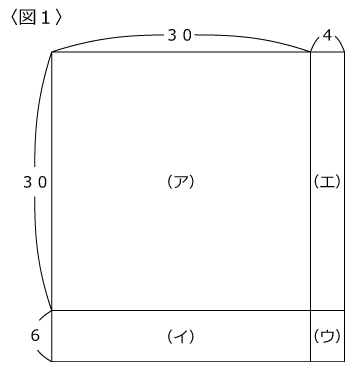
（エ）を（イ）にくっつけたのが〈図２〉です。

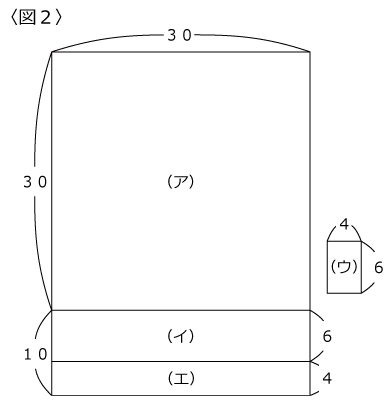
〈図２〉を使って計算するならば

３０×（３０＋１０）＋４×６
のようになりますが、これを変形すると
３０×４０＋４×６
＝（３×４）×１００＋４×６
となります。
ここから先がいかにもインド式なのですが、「×１００」というのは位を
２つ左にずらすことと同じですから、１２×１００は「百の位を基準にすれば」
１２ということになります。ですから最初の計算結果の上２ケタと
後の計算結果を並べて書いたものが答になるのです。
３×４×１００＋４×６＝１２２４　…（答）

どうですか？この形なら「インド式」でやってみたくなったのではないでしょうか。
今後、このやり方が使えるシーンが何度もあるはずなので、逃さないように
準備しておきましょう。

具体的な算数の問題に関するご質問など、お子様の中学受験に関してお困りの点がございましたら、こちらのフォームからご質問を承ります。
お寄せいただいたご質問へは当ブログ上にてご回答させていただきます。