VOL.95【計算名人への道】インド式計算（３）　－平均と掛け算－

前回と前々回は「２桁×２桁」の掛け算でしたが、今回も似た形が基本になります。

例えば「７４×６６」のように、「２つの数の平均が切りがよくなる掛け算」を取り上げます。

「７４×６６」で説明していきます。
「７４」と「６６」の平均は「７０」で、「７４」は「７０」よりも「４」大きく、「６６」は「７０」よりも「４」小さいことを確認しておきます。

という要領で求めることができます。もう少しやってみます。

使えるケースは限られていますが、なかなかの威力だと思います。
これなら暗算でできそうですね。

例によって、なぜこのやり方ができるか考えてみます。
これまた面積図による説明です。

２３×１７を例にします。

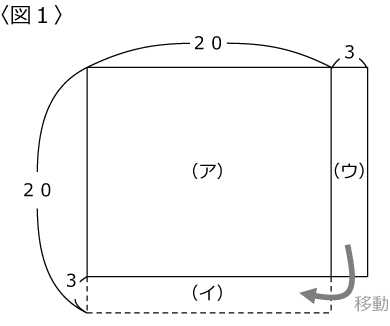
２３＝２０＋３，１７＝２０－３なので、〈図１〉の（ア）と（ウ）の面積の合計が答です。
（ウ）の長方形を（イ）のスペースに移動すると〈図２〉のようになります。

（イ）と（ウ）は縦の長さが同じで横は３だけ（ウ）が短いので、〈図２〉のように「３×３」の正方形の隙間ができることになります。
よって、「２３×１７」は１辺が２０（平均）の正方形から１辺が３（差）の正方形を引いたものになるので、

今回の計算は桁を問わないという強みがあります。
２数の平均が切りのよい数になるときは、是非このやり方を試してください。
計算がグッと楽になりますよ。

具体的な算数の問題に関するご質問など、お子様の中学受験に関してお困りの点がございましたら、こちらのフォームからご質問を承ります。
お寄せいただいたご質問へは当ブログ上にてご回答させていただきます。