VOL.92【受験生との歩み】 灘編 -強みを生かす-
かなり昔になるのですが、講師としての自分のスタイルを模索していた時期がありました。
その時、漠然とイメージしたのが、難関校受験に強い講師になるというものでした。
そして、同一年度に御三家合格を三人出した時に、ある程度達成できたように思いました。
その頃から、もっと内容の濃い指導をしたいと思うようになっていました。
しかし、実際は生徒の志望校・実情に合わせた指導をするので、自分の好き勝手をするわけにはいきません。
目の前の授業を精一杯行う日々が続きました。
生徒に恵まれたこともあって、合格の実績も十分に積みあがりました。
ただ、自分の全てを出し切るような達成感を味わうことはありませんでした。
小学生を相手に教えているので、当たり前なのかもしれませんが、もっと多くのことを生徒に伝えられるような気がしていたのです。
そんな希望がかなうはずもなく、数年が経ったあるとき、突然チャンスがやってきました。
松岡君(仮名)は「栄光志望」だったのですが、冬にお父さんの転勤が突然決まり、兵庫県の学校を受験することになりました。
ご家庭では急な志望校変更に対応することができず、思わず名門会の門を叩いたという流れだったと記憶しています。
候補は「六甲」「甲陽」「灘」で、偏差値的には「甲陽」が無難でした。
初回の授業を私が担当し見通しを立てました。
- 「算数」だけで判断するなら、「灘」は相当厳しいが可能性はある。
チャレンジする価値は大いにあると思う。 - 「算数」は2日間に分けて行われるが、ネックになりそうなのが「1日目」。
これの対策が間に合うかどうかで勝負が決まると思われる。 - 「2日目」の対策は今までの勉強の延長上にあるので、過去問演習と頻出分野の強化でなんとかなりそう。
といった内容の話をご両親にしたと記憶しています。
そこからのご両親の対応の速さには驚かされました。
翌日には塾を辞めて、受験まで名門会一本でいくことになりました。
入試本番まで2ヶ月を切っていましたから、全く余裕はありません。
幸い名門会1本になったので、十分な量の宿題を出すことができました。
授業では「1日目」の対策をメインに行いました。
まずは古い「過去問」約15年分を分野別に編集し直したものをやりました。
このとき苦戦したのが「場合の数」「文章題」で「平面図形」「立体図形」「速さ」は良好でした。
『「図形」に強いことを生かし、「場合の数」には目をつぶる』
というのが最後まで徹底した方針で、時間がない中での最善の戦略だったと思います。
次いで、新しめの「過去問」10年分を特殊なやり方で行いました。
時間をはかり、ある程度まで進んだところで、私と少し話してから続きをやるというものでしたが、私の狙っていた効果は感じられました。
それと並行して「2日目」対策を行いました。
「過去問」は宿題にし、わからなかった問題の解説を行いました。
また、「頻出分野」は私が「プリント」を用意し、最高難度の問題に取り組みました。
宿題は「過去問」以外に
- 基本的な解法を網羅した問題集
- オリジナルテスト
を毎日やるように指示しました。
松岡君が素晴らしかったのは、時間の管理がしっかりしていたことです。
直前期は自習の時間も長かったのですが、よく集中できていたと思います。
このような指導の甲斐もあって、過去問の点数にはかなり余裕がでてきた矢先、大きな不安材料が発覚しました。
本番の1週間ほど前、奈良県の学校を受験したのですが、内容があまり良くありませんでした。
答案をチェックすると算数の点数があまり伸びていませんでした。
密かに満点を期待していたので少しだけがっかりしました。
何があったのかチェックすると、今まで見たことのないようなミスを連発していました。
その時私が出した結論は「緊張しやすいタイプ」だったというものでした。
今でも覚えていますが、そのような結論に至った瞬間、目の前が一瞬真っ白になりました。
自分にとっても最大の目標だった「灘合格」が果てしなく遠いものに感じられました。
しかし、それは「一瞬」でした。
次の瞬間から、合格へ向けての闘志は以前よりも激しくなっていたと思います。
「この気持ちは必ず松岡君に伝わるはず。そして、ここぞという時の力になるはず。」
という思いを込めて、最後の1週間の授業を行いました。
全ての授業を終えた後、
「自分の持っているもの全てを伝えることができた」
という満足感に包まれました。
(「単なる“自己満”だろ」というお叱りを受けそうですが、合格につながる“自己満”ということでご容赦願います。)
結果は合格。
最初の授業の時の見通しそのままに事が運び、合格という結果を得ることができた、稀なケースだったと思います。
【受験生との歩み】と題して12人の合格までの軌跡を紹介しました。
皆様の参考になったでしょうか。
次はいよいよあなたの番です。
このブログを読んでいればアドバンテージは十分です。
自信を持って試験に臨んでください。
今回を持ちまして現6年生向けの内容は一区切りとさせていただきます。
今までお付き合いいただきまして、どうもありがとうございました。
具体的な算数の問題に関するご質問など、お子様の中学受験に関してお困りの点がございましたら、こちらのフォームからご質問を承ります。
お寄せいただいたご質問へは当ブログ上にてご回答させていただきます。
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の1題立体図形
難易度★★★★★
〈図1〉は、AB=AD=10cm、AE=9cmの直方体です。
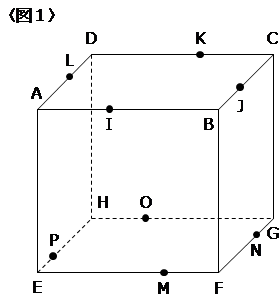
また、AI=BJ=CK=DL=4cm、EM=FN=GO=HP=7cmです。
この直方体を次の8組の3点
(I,M,J)(J,N,K)(K,O,L)(L,P,I)
(I,P,M)(J,M,N)(K,N,O)(L,O,P)
をそれぞれ通る8つの平面で切断し、正方形IJKLを含む立体をVとします。
(1)立体Vの体積は何cm2ですか。
(2)立体Vを辺AEの中点を通り、正方形IJKLと平行な面で切断したときの切り口の面積は何cm2ですか。
(3)〈図1〉で、三角すいB-IMJを考えます。
三角形IMJを底面としたときの高さは何cmですか。
ただし、3辺の長さが3cm、4cm、5cmの三角形は直角三角形です。
また、必要ならば〈図2〉使用してもかまいません。
解答が表示されます













