VOL.86【受験生との歩み】 慶應編(2)
来年の「慶應湘南藤沢」の受験は難しいものになるかもしれません。
募集人員の減少と英語選択入試の導入により、今までとは異なった様相となるでしょう。
一般入試の定員が120名から70名に減り、そこに新たに英語選択が加わるので、4教科受験の受験生にとってより狭き門となることは数字の上からは明らかです。
一部の塾では難化が予想され敬遠されるだろうから、むしろ狙い目という話も出ているようですが、こればかりはふたを開けてみなければわかりません。
来年SFCを受験するにはそれなりの覚悟が必要となるのではないでしょうか。
今回振り返る受験生は、仮に来年受験するとしても自信を持って送り出せる、そんな優秀な生徒です。
本田さん(仮名)は算数が得意で得点源でした。
ところが秋の模試であまり振るわず、偏差値も60台前半と不本意なものでした。
例によってこのようなタイミングで私が引き受けたのですが、特に不調といった印象は受けませんでした。
ですから、普通に授業を進めることにしました。
普通の授業とは
①問題を解く(すんなり解ければそこで終了→次の問題へ)
②私が考え方の方向を示す(どこかのタイミングで解けそうなら自力で解く→次の問題へ)
③一緒に検討する(大抵は私がリードすることに)
④自力で解いてみる
という流れです。
気をつけなければいけないのは①での正解率で、正解ばかりだと、私が単なる生徒の自習に付き合っているおじさんになってしまいます。
かといって1問もできないと生徒のモチベーションが下がってしまうでしょう。
本田さんの授業では正解率50%を想定して教材を用意したのですが、実際はもっと高い正解率でした。
私にとっては「単なるおじさん」になってしまう危機だったのですが、そうはなりませんでした。
それは本田さんの意識が高かったからです。
一部の生徒にみられるあまり良くない姿勢として、「正解できればそれで良い」とするものがあります。
具体的には
- 正解した問題について別解を解説しても聞く耳を持たない
- 一度習った解法に固執し、新しい解法にチャレンジしようとしない
- その問題の本質を理解するために頭を使うということをしない
ということが挙げられます。
算数ができる生徒というのは「別解の研究」「新しい解法の追求」「本質を理解する努力」を自ら積極的に行っています。
上の悪い例の真逆ですね。
ただ、「正解できればそれで良い」というのは、ドライに「点数」を追い求めた結果と考えることもできます。
ということは、現在の大手塾でみられるようなテスト漬けの環境が、算数が苦手な受験生を生み出している原因の一部なのかもしれません。
話を本田さんに戻します。
本田さんは意識が高い上に、人の話に耳を貸す素直さも持ち合わせていました。
ですから、正解した問題に対して私が別解を示しても、嫌な顔をするどころか随分と感心していたことを覚えています。
実は、1対1で授業をしているとこの「リアクション」で、生徒の「理解度」や「定着度」が大体わかります。
この時の反応が薄いと「理解度」はともかくとして「定着度」が低いことがほとんどです。
※実際は反応には個人差があるので、他の情報を加味して定着度を予想するというのが本当のところです。
1問1問丁寧にみていくと、彼女ほどできる生徒でも解法が私と同じをいうことはほとんどなく、ほぼ全ての問題で図の描き方やよりスマートな解法についての解説を行えたので、かなり内容の濃い授業となりました。
また、彼女は頭の回転が速かったので、10の内容を説明するのに2~4程度まで説明すれば良いことが多く、通常の3倍近くの量をこなすことができました。
1ヶ月ほど指導した後に模試があったのですが、算数の偏差値は75を超えていました。
その後の成績は多少の上がり下がりはあったものの、算数に関しては十分に仕上がった状態で本番を迎えることとなりました。
実は本番前にマイナス材料がありました。
- 社会が今一つ仕上がっていない
- 後でわかったのだが、1月の終わりにインフルエンザを発症していた
これらを克服して第一志望の「慶應湘南藤沢」に見事合格という結果でした。
そんな彼女でも算数は満点ではなかったそうです。
最後の問題がわからなかったとのことでした。
私としてはそれが少し悔しかったですが、それは贅沢というものでしょう。
充実した授業は今でも良い思い出として、私の中に残っています。
具体的な算数の問題に関するご質問など、お子様の中学受験に関してお困りの点がございましたら、こちらのフォームからご質問を承ります。
お寄せいただいたご質問へは当ブログ上にてご回答させていただきます。
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の1題水・食塩水
難易度★★★★☆
〈図1〉のような直方体の水そうに、底面と垂直になるような長方形のしきり板P(高さ30cm)とQ(高さ40cm)の2枚を入れて底面を3つの長方形に分け、それを左から(あ)、(い)、(う)とします。
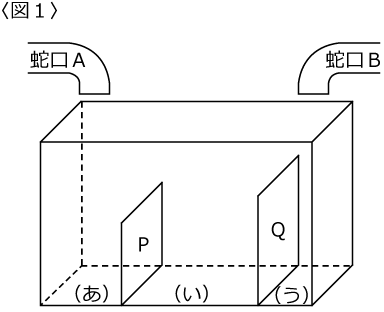
また、水そうを満タンにすると600Lの水が入り、水位は60cmになります。
蛇口Aからは(あ)の部分に一定の割合で水を注ぐことができます。
蛇口Bからは(う)の部分に一定の割合で濃度20%の食塩水を注ぐことができます。
蛇口Aと蛇口Bから体積が7:6の割合になるように注水し、(い)の部分の水位が18cmになったところで注水をやめて、(い)の部分をよく混ぜて食塩水の濃度を調べると10%でした。
次に、1度水そうを空にして、蛇口Aと蛇口Bから体積が23:32の割合になるように注水し、(い)の部分の水位が21cmになったところで注水をやめて、(い)の部分をよく混ぜて食塩水の濃度を調べると16%でした。
※しきり板の体積は無いものとします。
※水1gの体積は1cm3とし、食塩を水に溶かしても体積は変化しないものとします。
例えば、90gの水に食塩10gを溶かすと、体積は90cm3、濃度は10%です。
(1)(あ)と(い)と(う)の面積比を求めてください。
(2)下の に入る数を求めてください。
水そうが空の状態から、蛇口Aと蛇口Bから体積が3:2の割合になるように注水し、(い)の部分の水位が30cmになったところで注水をやめて、(い)の部分をよく混ぜてから、水位が cmになるように(い)の部分の食塩水を汲み出しました。
その後、3:2の割合で注水を再開し、水そうが満タンになったところで注水をやめ、しきり板を外して88kgの食塩を加えてから全体をよく混ぜて濃度を調べると20%でした。
解答が表示されます













