VOL.79【得点力アップ講座】(4)立体図形攻略
前回の本文中に約数の個数についての記述がありましたが、少し説明不足だったかなと思い、補足することにしました。
約数の個数の計算方法は、
① 素因数分解する
② 使われた素数ごとに個数をカウント
③ ②の数字全てに1を足す
④ ③の数字全てを掛け合わせる
という手順でした。これを理解していれば約数の個数から元の数を絞り込むことができます。
1個…1
2個…素数
3個…素数の2乗(2回掛け合わせたもの)
4個…(異なる)素数×素数,素数の3乗
5個…素数の4乗
前回の本文中の(例題)で取り上げたのは4個のケースだったので、「素数×素数」か「素数の3乗」の可能性があったのですが、「900台」に「素数の3乗」はないことは明白なので、無視した記述になっていました。
それでは、今日も点数を稼いでいきましょう!
◎【得点力アップ講座】(4)立体図形攻略
苦手分野のアンケートをとれば「立体図形」が上位にくると予想されます。
実際、指導していて「立体図形」が最初から得意な生徒に出会ったことはあまりありません。
多くの受験生が苦手としている分野を得意にすることができれば、他の受験生に大きく差をつけられるかもしれません。
「立体図形」はチャレンジする価値が高い分野と言えそうです。
まず、難しくなる原因について考えてみます。
① 次元のずれ
出題する際は紙の上ですから、3次元のものが2次元に置き換わって出題されることが多いです。
中には言葉だけで出題されるような問題もあります。
(例)立方体の各面の対角線の交点6個を頂点とする立体の体積は元の立方体の何倍か。
つまり、出題者の頭の中にある「立体」が再現できるような情報が与えられ、その情報を元に受験生は自分の頭の中に「立体」を作らなければならないのです。
問題を認識する際にどうしてもひと手間かかってしまうのが「立体図形」の特徴といえるでしょう。
② 数字が大きくなりがち
特に体積の計算でおきるのが、数字が大きくなることです。
底面積に高さを掛けることになるので、面積の計算よりも1、2桁大きくなることが多いです。
数字が大きくなると計算ミスの可能性も大きくなるので、気をつかわなければなりません。
③ 公式が多い
立体図形特有の公式はそれほど多くないですが、平面図形の公式は全てマスターしていることが前提になるので、負担が増えることに変わりありません。
特に円すいの公式が「わかっていない」、あるいは「使いこなせていない」ケースが目立ちます。
覚えていることも大切ですが、なぜそうなるのかの理解も大事なので、少しでも不安があるようでしたら、指導者に質問することをおすすめします。
④ 覚えることが多い
公式が多いことと同じような問題です。
例えば「立方体の積み木」だったら「輪切り方式」、水の問題だったら「面積図」といった具合に有効な解法は存在するのですが、それを記憶しなければなりません。
ほんの少しの違いが解法に影響を与えるので、そのあたりの記憶を負担に感じる受験生も多数存在するでしょう。
⑤ そもそも何をどうやったら良いかわからない
いわゆる「手も足も出ない」状態です。
試験会場でこのような状態になってしまったらひとまず他の問題に移れば良いだけです。
無駄に時間を使わないように注意しましょう。
普段の勉強中にこのような問題に遭遇した場合も、無理に解こうと頑張る必要はありません。
指導者に質問するか、答を見ましょう。
さて、①~⑤までいかにもありそうですが、どれもきちんと勉強していれば克服できそうです。
「立体図形」をきちんと勉強する方法をまとめたいと思います。
① 正確な作図
「見取り図」、「展開図」、「投影図」等を正確に描けるように練習しておく必要があります。
ここで注意が必要なのは、「解くための作図」と「理解するための作図」は必ずしも一致しないということです。
例として、ある軸のまわりを三角形や四角形が1回転したときにできる図形の求積について考えます。
学習当初は感じをつかむために必ず「見取り図」を描いていたと思います。
しかし、長方形が円柱、直角三角形が円すいになることが完全にわかってしまえば後は組合せの問題となります。
計算するのに必要な数値は回転させる前の長方形や直角三角形に書き込んだほうがわかり易いかもしれません。
私の感覚では、回転体の求積は「見取り図」を描く必要がないばかりか、描いたら損するとさえ思っています。
また、「立方体の積み木」の場合、「見取り図」を描きたいこともありますが、描くのが大変なケースが結構多いです。
こちらは必要ないというよりも描くのがあまり大変だと損してしまうので、なるべく描きたくないといったところでしょうか。
勿論普段の学習で時間的に余裕があるならば、多少面倒なものでもしっかり描けるように練習すべきでしょうが、時間を点数に変えるという観点からはあまり効率が良くないでしょう。
何も考えずに作図を開始するのではなく、明確な目的を持って作図を行えるようにしたいですね。
② 知識の充実
算数の問題は基本的に、知っていれば簡単ですが、1から自分の頭で考えるとかなり大変です。
ですから知識はとても大切で、できる限り頭に入れておきたいのです。
「図形問題」の場合「形」で分類することができるので、やったことを点数に替えやすい分野のような気がします。
ただ、再三言っていることですが、「丸暗記」は使い物にならないので絶対にやってはいけません。
記憶する場合は必ず「理解を伴った」ものにしてください。
「理解」をするように頑張っていたら自然に覚えてしまった、というのが理想だと思います。
③ 比を利用する
「平面図形」でもそうでしたが、「相似な図形」が出てきたときは「比」の利用がカギとなります。
「比」を使えばある程度数字が大きくなるのを抑えられるので、計算ミスのリスクも軽減されます。
円周率が関係する問題も「比」を使って煩雑さを緩和できる可能性があります。
「立方体の切断」の問題で体積を求めるケースでは完成形の三角すいから部分を引いて求めることがよくありますが、この時、各三角すいが相似になるので「体積比」を使ってスマートに計算することができます。
④ 実物を観察する
頭の中だけだった存在を手に取って観察できれば、一気に理解が深まります。
例えば、四角すいを斜めに切った図形の体積を求めるようなケースでは、四角すいを2つに切って三角すい2個と考えれば解決ですが、頭の中だけではなかなか理解できないかもしれません。
そんな時、問題に出てくる立体の模型を手に取ることができれば、頭の中のモヤモヤがすっきりと晴れて、やる気もわいてくることでしょう。
私は授業で使う模型をある程度ストックしているので、よくわからないケースもすっきりと解決できることが多いです。
模型は本人が作るわけにはいかないので、市販されているものを利用するか、指導者に作ってもらうか、保護者が作るかの選択になると思います。
私の模型が皆さんに行き渡れば良いのですが・・・。
⑤ 自信を持つ
「立体図形」と言えども解くのが無理な問題というわけではありません。
出題者の心理は「問題を解いて欲しい」のです。
(私は毎週問題を出しているのでよくわかります。)
ですから「きちんと勉強したんだから必ず解ける」という自信を持って試験に臨んでください。
試験会場では色々ありますが、仮にどうしても解けない場合は「自分が解けないのだから他の人が解けるはずがない」と考えてしまってかまいません。
算数は自信がある人に良いことがある科目であると私は考えています。
プラス思考でいきましょう。
ただし自信の裏づけとなる「勉強量」は必要です。日々の努力が自信につながるのです。
以上のようなことに留意して勉強を進めていけば、「立体」を見ただけで逃げ出したくなるようなことはなくなるでしょう。
そして、「立体図形」に対して「解ける」という自信が生まれてくれば、得点力が大幅にアップすること請け合いです。
具体的な算数の問題に関するご質問など、お子様の中学受験に関してお困りの点がございましたら、こちらのフォームからご質問を承ります。
お寄せいただいたご質問へは当ブログ上にてご回答させていただきます。
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の1題立体図形
難易度★★★★★
〈図1〉は平らな土地の上に直角二等辺三角形ABCと長方形CDEAが接している様子を表しています。
DE上の点Fは点Dから2mのところにあります。
今、〈図2〉のような展開図の板を組み立てて(これを物体Pとします)、〈図3〉のように点A、点Bと重なるように置きました。
物体Pについては〈図2〉の斜線部の面積が6m2であることがわかっています。
また、〈図4〉のように、BF、BDとACとの交点をそれぞれG、Hとすると、GHの長さは11 3 mでした。
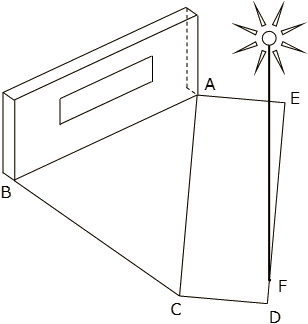
点Dと点Fそれぞれから真っすぐ上に8.4mのところに電灯を設置し、物体Pを照らしたところ、できた影の面積の差が10m2でした。
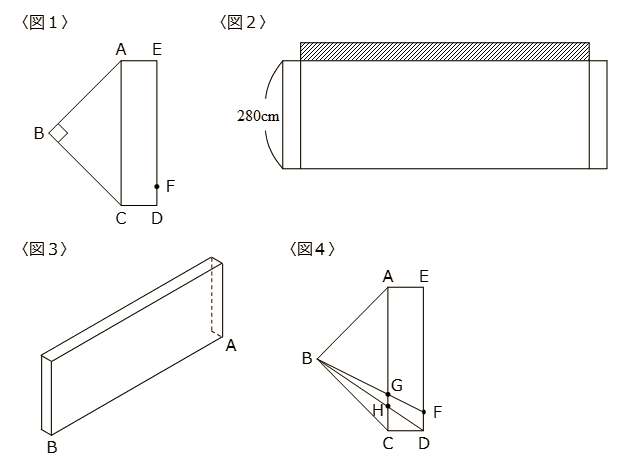
次に〈図5〉のように物体Pに穴をあけてから、点F上の電灯で物体Pを照らし、影を作りました。
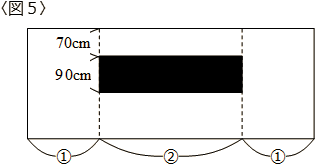
板の厚さ、電灯の大きさは考えないものとして、以下の問いに答えてください。
(1)ACとCDの長さをそれぞれ求めてください。
(2)物体Pに穴をあけた後の影の面積を求めてください。
解答が表示されます













