VOL.78【得点力アップ講座】(3)「わからないもの」の位置
皆さん、過去問やってますか?
いきなりですが、これからは過去問演習が大切です。
計画的に進めてください。
表を作ってそこに点数を書き込んでいくのがおすすめです。
だんだんと数字が埋まっていくのは楽しいですよ!
また、過去問を解く際は、「どうすれば点数を多く取れるか」ということを意識してください。
繰り返しになりますが、具体的には
①計算ミスをしない。
②問題文をよく読み、正確に答える。
③検算、吟味を適切に行う。
④時間配分を誤らない。
の4点に気を配ってください。
自分にとってどうするのがベストなのか色々と実験して、確実に仕上げていきましょう。
◎【得点力アップ講座】(3)「わからないもの」の位置
算数の問題は基本的に、何か「わからないもの」が他の「わかっているもの」から求められるように作られています。
この「わからないもの」の数が増えるとその問題は難しくなります。
「ニュートン算」を難しく感じる受験生が多いのは普通の「仕事算」に比べて「わからないもの」が多いからです。
この「わからないもの」は量以外に「位置」の問題があります。
例えば「割合」の問題の場合、3量のうちの2つがわかれば解けるので、「わからないもの」の位置が3通りあると考えられます。
「割合」や「速さ」の公式が3つあるのはこのことに対応していると言えます。
「割合」「速さ」の公式を使うものは大丈夫ですが、「わからないもの」の位置が「基本問題」とは「異なる位置」になることによって難しくなる問題もあります。
例として「平均の問題」を取り上げます。
<基本問題>
3回テストを受けて平均点が70点でした。
次のテストで78点を取ると平均点は何点になりますか。
<位置が異なる>
何回かテストを受けて平均点が70点でした。
次のテストで78点を取ると平均点が72点になるといいます。
今までに何回テストを受けましたか。
<基本問題>は平均の「定義(個々を全て足し合わせ個数で割った値 )」をそのまま使えば解けます。
ところが、<位置が異なる>場合、何回テストを受けたかわからないので、「全て足し合わせた値」がいくつなのかわかりません。
「定義」を知っているだけでは解けない問題なんですね。
実際は「面積図」を描くなどして「逆比」を使って解きますが、この問題も「基本」の範囲です。
ここで、知っておいて欲しいのは、「面積図」を描けば両方とも解けるということです。
「異なる位置」に対応できる解法は「基本の位置」の問題にも対応できる可能性が高いです。
なので、「平均の問題は面積図で解く」というように対応できる範囲が広いほうに自分のスタイルを決めておくと良いと思います。
さて、この「位置」の問題で最もやっかいなのが、解が複数個になるケースです。
例えば
「6の約数の個数を求めよ。」
の「わからないもの」の位置を変えると
「整数Aの約数の個数は4個である。Aを求めよ。」
となりますが、ヒントがこれだけだと問題として成立していないレベルでしょう(無限にありますから)。
必然的に別の要素が入ってきて複雑になり、難易度も増すことになります。
ひとつ例題を作ってみます。
<例題>
3桁の整数Aの約数の個数は4個です。
またAの各位に使われている数字の合計は14です。
Aとして考えられるものの中で3番目に大きなものを求めて下さい。
(答)905
どうですか。
かなり面倒なことになっていたと思います。
950から順番に調べていけば良いのですが
923=13×71
914=2×457
905=5×181
の素因数分解を全部やり
(71、457、181が全部素数であることの確認が必要)
やっと正解にたどり着きます。
このように、解が複数になるものが別の要素で絞りこまれ、問題として成立するようなケースでは難易度が高めになります。
では対策に移りましょう。
カギは普段の勉強にあります。
時間は限られていますから、勉強の「質」を上げることが大切です。
「理解→記憶→演習→定着」という過程の中で、特に「理解」に力を入れるべきです。
その「理解」を深めるのに、この「わからないものの位置が異なる」問題が役に立ちます。
いつもと位置が異なるので、その問題の本質が理解できていないとわからなくなる可能性が高いわけです。
本当に理解できているかどうかのチェックができるのですね。
また、解法に幅がないと対応できないことがあるので、そちらのチェックにもなります。
さきほどの例題だと、約数の個数を書き出しでしか求められないと正解にたどり着く前に息切れしそうです。
約数が4個の整数は(素数×素数)であることを知っていれば、労力はかなり減るでしょう。
そして、普段の勉強では、なぜ(素数×素数)であらわすことができる整数の約数の個数は4個なのか理解をし、約数の個数は素因数分解を利用して求めると決めておく。
ここまでやっておけば「質」の高い勉強と言えるでしょう。
また、「解が複数個あるケース」は公式を覚えていれば解けるようなものではありません。
自分の手を動かして、調べて、考えて、ということが必要になります。
これこそが本来の「算数」の勉強と言えるかもしれません。
集中力を高めて取り組んで欲しいと思います。
まとめます。
- 普段の勉強で特に気をつけたいのは理解の「質」を高めること。
- 「わからないものの位置が異なる」問題は、その問題の本質が理解できていないと解けないことが多いので、理解度のチェックの機能がある。
また、解法に制約が出てくることもあるので、解法の選択の基準になる。 - 解が複数になるケースもあり、この場合は書いて調べることになる。
自分の手を動かす練習ができる「貴重な問題」である。
結局今回は
「【得点力アップ講座】(1)いつもと何か違う!?」
の具体例のようなテーマでしたが、「本質の理解」「解法の選択」「手を動かす」という重要な項目と関係するので、独立した論点として取り上げました。
過去問を解いていて、このような「異なる位置」の問題が多いと感じたら、早速理解の「質」を高めることを実践しましょう。
ライバルに差をつけるチャンスかもしれませんよ。
「わからないものの位置が異なる」問題を通して、理解の「質」を高めれば、得点力がアップすること請け合いです。
具体的な算数の問題に関するご質問など、お子様の中学受験に関してお困りの点がございましたら、こちらのフォームからご質問を承ります。
お寄せいただいたご質問へは当ブログ上にてご回答させていただきます。
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の1題整数問題
難易度★★★★☆
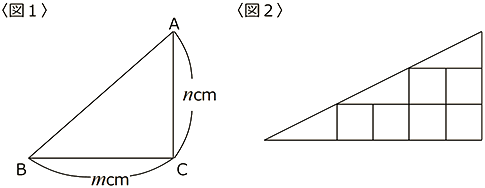
〈図1〉のように、底辺がmcm、高さがncmの直角三角形ABCがあります。
ただし、m、nはともに整数で、m>nです。
この三角形の内部に1辺が1cmの正方形を何枚しきつめられるかを考え、その最大値をkとすることとします。
〈図2〉は m=6,n=3のとき、k=6であることを示しています。
(1)m=100,n=81のとき、kはいくつになりますか。
(2)k=57のとき、mとnの組合せとして考えられるもの全てを、(m,n)の形で答えてください。
解答が表示されます
(2)(115,2)(58,3)(57,3)
(39,4)(20,7)(15,9)













