VOL.77【得点力アップ講座】(2)平面図形を得意分野にしよう!
前回のブログで「得点力アップ」のためには「算数の力」をつければ良いと書きました。
そして「算数の力」をつけるためには、いつもと違う問題に出くわした時に「手を動かして調べ、自分の頭で考える」ことをお勧めしました。
ここでひとつ補足しておきますが、「全く見たことがない問題」や「全くわからない問題」には、あまり時間をかけてはいけません。
理由は2つあります。
ひとつは時間がもったいないこと、もうひとつは考えるための材料がない状態でいくら頑張っても脳が働かないので、思考力を鍛えることにならないことです。
少し考えてわからなければすぐに答を見てください。
そして解説を読んで理解しましょう。
そうすればその問題は既知の問題となるので、次に似た問題に出くわした時に解ける可能性が出てきます。
◎【得点力アップ講座】(2)平面図形を得意分野にしよう!
この講座は、夏休みを終え、ある程度「基本」がしっかりした受験生がさらに上を目指す際、どういったことに気をつければ良いかを中心に書いていこうと思います。
基本ができているということは「苦手分野」はないということが前提になります。
もし「苦手分野」がまだあるのならば早急に手を打って下さい。
さて、「苦手分野」はないけれど「得意分野」もないという受験生はどの分野から強くしていったらよいのでしょうか。
それはズバリ「平面図形」です。
このブログの中でも「平面図形」のできることの優位性を書いてきましたが、今回改めてそのことについて検討してみたいと思います。
既に過去問演習を開始している受験生が大半だと思います。
その際、「図形問題」の割合がどれくらいかを把握しておくと、普段の勉強で「図形」にどれくらいの比重を置けばよいかが見えてくると思います。
学校によっては「図形」の占める割合が5割以上ということもあります。
習う単元に対する「図形」の割合よりも、出題率が上回っていることが多いような気がします。
この事実だけでも「図形」は強化しなければならないということになるでしょう。
さらに、「図形問題」は解法が浮かぶか浮かばないかが明暗を分けるケースが多く、分かってしまえばその後の処理は楽なことが多いです。
つまり、できる側の人間にとってはサッと解けて時間をあまり使わない「おいしい問題」なのですが、できない側の人間にとっては、解法を思いつかなければ解けないし、仮に思いついたとしてもそれなりに時間がかかってしまう「危険な問題」と化してしまうのです。
「図形」を「平面図形」「立体図形」「動く図形」の3つの分野に分けた場合、上記の「時間的アドヴァンテージ」を最も受けやすいのは「立体図形」だと思います。
「平面図形」はどこまで行ってもわからないものはわからないという側面がありますし、「動く図形」は「作図」という作業がありますから、そこの部分ではあまり時間短縮が見込めません。
では「立体図形」から取り組めば良いかというとそうではなく、まずは「平面図形」というのがものの順序だと思います。
「立体図形」ができるようになるコツは、次数を落として平面的にとらえることなので、「平面図形」の力がなければなりません。
「平面図形」は苦手だけど「立体図形」は得意という生徒に会ったことはほとんどありません。
また、「動く図形」も作図が終われば「平面図形」ですから、「平面図形」の力は「図形全般」に及ぶと考えられます。
以上のように「平面図形」を得意分野にすれば「図形全般」に好影響を与えることは分かってもらえたと思います。
じつは「平面図形」ができるようになれば「数量」の分野にも良いことがあります。
特に試験においてなのですが、「数量」の分野は計算が複雑になることも多く、時間とのたたかいという側面が強いのです。
そうなると「図形分野」で獲得した余剰時間を「数量分野」にまわすことができるということが大きなメリットになります。
常に不足気味な時間の中で問題を解くのと、ある程度時間的な余裕がある状態では、正解率が変わってくるでしょう。
最後に「平面図形」が得意であることを試験の点数に変える方法を考えます。
どの問題から解いていくかという解答順が、試験では特に大切です。
原則的には解けそうなものから解いていくのが良いと思います。
当然個人差があり、「計算問題」から入る者もいれば、「特殊算」からという受験生もいるでしょう。
少なくとも前から順番というのはあまりお勧めできません。
早い時期に「図形問題」が解けると、流れが良くなることが多く、私のお勧めになります。
問題によっては「一瞬」で解けることもあり、これが意外と大きいです。
試験開始当初はまだ「脳」が温まってない状態です。
それが問題を解くことによって徐々に温まっていきます。
ところが「図形問題」が「一瞬で解ける」と「脳」の回転速度が一気に上がるような感覚になります。
いわゆる“乗っている”状態に一気になるわけです。
そうなると益々「一瞬で解ける問題」が増え、十分な時間的余裕が生じると思われます。
「図形問題」でほぼ決着をつけてしまえば、他の問題に対しても十分に実力を発揮できるというわけです。
「平面図形」を突破口にして「図形問題」を攻略し、試験での点数の大幅アップを目指しましょう。
具体的な算数の問題に関するご質問など、お子様の中学受験に関してお困りの点がございましたら、こちらのフォームからご質問を承ります。
お寄せいただいたご質問へは当ブログ上にてご回答させていただきます。
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の1題平面図形
難易度★★★☆☆
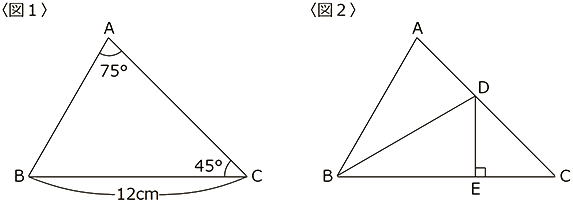
〈図1〉の三角形ABCにおいて
∠A=75°
∠C=45°
BC=12cm
です。
また〈図2〉は三角形ABCの辺AC上に
AB=DBとなるように点Dをとり、点Dから辺BCに垂線を下ろし、
その交点をEとした様子を示しています。
(1)三角形ABDと三角形DECの面積比を求めてください。
(2)四角形ABEDの面積を求めて下さい。
解答が表示されます













