VOL.16平面図形
先週（ブログvol.１５＜６/２３号＞）の問題はいかがでしたでしょうか。
前から気になっていたことを問題にしてみました。
ほんの少し設定を変えただけで、やらなければいけないことがかなり増えたと思います。
自力で解き方を思いつくのは難しいと判断したので、（１）がヒントになるようにしました。
皆さん、ヒントに気づきましたか？
難しい問題はノーヒントではほとんどの人が解けないので、誘導が付いているケースが多いです。その誘導に乗るというのも大切な技術です。
是非身につけるようにしましょう。
今週のテーマは『平面図形』です。まずはワンポイントアドバイスから。
| 角度 | 「外角の定理」は便利です。狙いを定めて角度を求めましょう。 |
|---|---|
| 面積 | 三角形・四角形・円・おうぎ形しか面積を求めることができないので、これらのうちのどの公式を使うのか考えましょう。等積変形、分割、和・差、移動等を用います。おうぎ形の面積は公式がふたつあるので、要チェックです。 |
| 面積比 | 三角形同士は高さが共通な場合、底辺の比がそのまま面積比です。底辺と高さの比がわかれば、その積が面積比です。相似比と面積比の関係も確認しておきましょう。 |
| おり紙 | 折ったら開くのがポイントです。長方形を折るとひし形ができやすいことは知っておきましょう。合同な長方形を重ねたときもひし形ができます。 |
| 平面の影 | 平面で考えます。複数の方向から見た平面図を書きましょう。 |
| 平行線の相似 | 「砂時計型」と「ピラミッド型」の相似は瞬時に見えるようにトレーニングしておきましょう。切って移動して整形すると良い場合もあります。 |
| 図形の重なり | パズル感覚で楽しみながら解きましょう。わかっているところから少しずつほぐしていくイメージです。 |
図形は得意・不得意がはっきりしやすい分野です。
平面図形が苦手だと立体図形も厳しくなるでしょうし、図形の移動や、規則性・場合の数にも影響が出るかもしれません。
算数である程度点数を稼ぎたいのであれば、平面図形は得意分野にする必要があるでしょう。
図形は先天的なセンスがなければ解けないわけではありません。
図形的なセンスは努力することで手に入れることが十分可能です。
私のおすすめのやり方を書きます。
「形」である程度解法が決まっているので、まずそれを頭に入れます。
例えば、「円（おうぎ形）がでてきたら中心をマークし、円周上の点（複数）と中心を結ぶ。すると必ず二等辺三角形ができるので、その低角が等しいことを利用する。」、「直角三角形が出てきたら相似・合同ができやすい。なければつくる。」などです。
あとはひたすら「形」から解法を見抜く練習をします。
この練習を繰り返しやっていると、あるとき変化が訪れます。
例えば、補助線を引いていないのに既に引いてあるように見えたり、簡単に綺麗な形に整形できたりと、今までの苦労が嘘のようにあっさりと解決できることが増えます。
こうなれば図形が得意分野になる道が拓けたと言ってよいでしょう。
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の1題面積
難易度★★★★☆
正方形ＡＢＣＤの各辺を５等分し、〈図１〉と〈図２〉のように結びました。 〈図１〉 線分ＰＱ上の各交点を順にＲ、Ｓ、Ｔとします。 〈図２〉 正方形ＥＦＧＨの面積は７１５ｃｍ２です。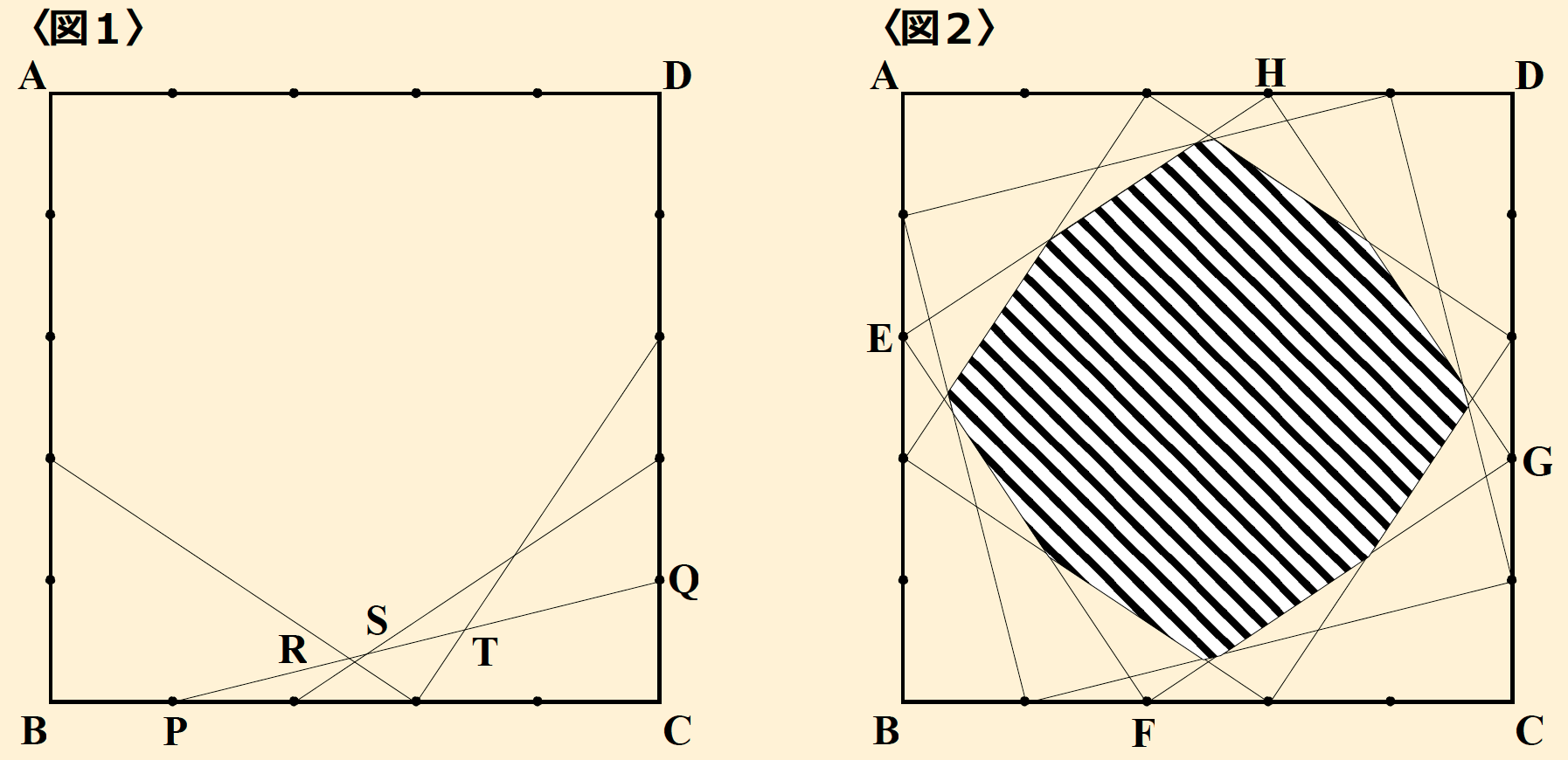 
（１）〈図１〉のＰＲ：ＲＳ：ＳＴ：ＴＱを求めてください。 （２）〈図２〉の斜線部の面積を求めてください。
解答が表示されます
