VOL.72【ミニ講座】(9)作図の手順 (10)21ゲーム
今回も内容が盛りだくさんです。
「ミニ講座」は書くのが楽しいのでどんどんボリュームが増えていきます。
秋以降も続けたいなぁ、なんて考え始めています。
皆様のご意見をお待ちしています。
◎【ミニ講座】(9) 作図の手順
「図形の移動」の問題は「作図」が肝心です。
特に何かが「ころがる」ようなケースでは、「作図」がキチンとできれば解けたも同然ですが、そうでない場合は苦戦が予想されます。
そこで、今回は「作図の手順」について説明したいと思います。
生徒が「作図」をしているのを見ていていつも思うのは、「色々なことをいっぺんにやろうとして無理が生じている」ということです。
複数のことを一緒にやろうとしてもうまくいかないことの方が多いです。
やはり、正しい手順で無理なく進めるようにしなければいけません。
直線上を長方形がころがり、頂点が動いた距離を求める問題を例に、作図の手順を説明します。
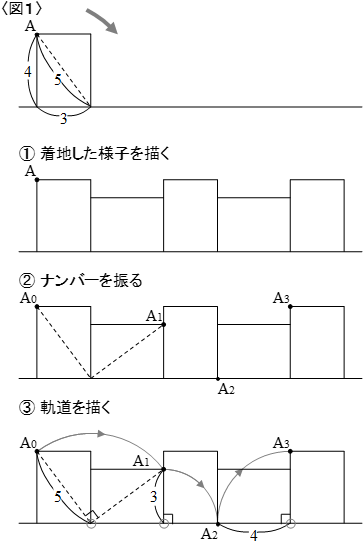
尚、作図の様子は下の〈図1〉に示しました。
基本的に作図の工程は3つに分けます。
①着地した様子を描く直線と長方形が接している様子を描きます。
通常は1個目と5個目が同じ向きになるので、最初の長方形を除くと4個の長方形を描くことになります。②求める頂点がそれぞれの長方形のどこにくるのかを確認しナンバーをふる頂点Aが動いた距離を求めるのなら、とりあえず頂点Aだけを追いかけます。
私の場合、最初をA0とし、以下A1、A2、A3…とナンバーをふっていきます。
③求める頂点の軌道を描くここが一番肝心なところです。
①と②は③のための準備だったとも言えます。
いっぺんにやろうとして失敗するというのは①、②をすっ飛ばしていきなり③をやろうとして失敗するということです。
この軌道は円周の一部となることが多いので、その場合は以下の3つを意識して作図していきます。
- 中心
- 半径
- 中心角
慣れないうちは中心を丸で囲んでしっかり意識するようにします。
半径と中心角は計算の際必要となる数字になるので、見にくくならないよう図の中に書き入れておきましょう。
ここまで手順にそってやっていけば、正解できる可能性は相当高いと思います。
無理のない手順で作図する方法を身につけてください。
ここで気をつけて欲しいのは「できる限り正確な作図をこころがける」ということです。
よくあるのが「円」がつぶれてしまうことです。それを防ぐにはどうしたらよいかを書きます。
「円」を描くのは結構難しいです。
白紙に描くのは特に大変ですよね。
そこで「ガイド」を先に描いてあげます。
この「ガイド」は「円」に内接するものなら何でも良いのですが、おすすめは「正六角形」です。
また「半円」に限るならそれは「正三角形3個分」になりますからそれを利用しても良いです。
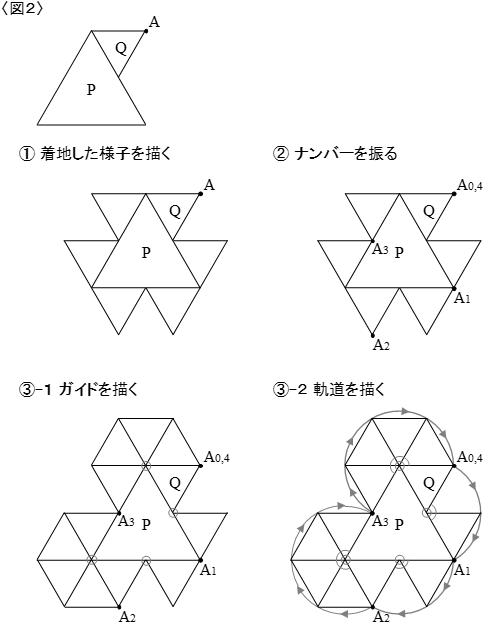
ではその「ガイド」を含めて、次の問題の作図の手順をごらんください。
<問題>
〈図2〉の1辺の長さが6cmの正三角形Pのまわりを、1辺の長さが3cmの正三角形Qがすべらないようにころがって正三角形Pのまわりを1周するとき、頂点Aが動く距離を求めてください。
ただし円周率は3.14とします。
(式)3×2×3.14× 120×2+240×2360 =37.68
(答)37.68cm
以上、「作図の手順」でした。
◎【ミニ講座】(10)21ゲーム
昔、友人から「21ゲームやろう」と誘われました。
何のことやらわかりませんでしたが、「いいよ」と答え、ゲームが始まりました。
ルールは簡単で1から順番に数字を言っていき21と言ったら負けという簡単なものでした。
一度に言える数字は1個から3個でパスはできないということでした。
以下その時の模様を再現(記憶があいまいですが)します。
友人: では最初は僕から「1」
金田: (よくわからないがとりあえず)「2」 ←この時点で負けが決定!
友人: (間髪入れずに)「3、4」
金田: 「5、6、7」
友人: 「8」
金田: (自信満々の友人の顔を見て、どうやら負けになっていると悟る)
以後、
金田: 「9、10」
友人: 「11、12」
金田: 「13」
友人: 「14、15、16」
金田: 「17」
友人: 「18、19、20」
金田: 「21」 ←負け!
金田: 負けました。もう一回やろう!
友人: いいよ。ではさっきは僕が先だったから、今度は君が先でいいよ。
金田: ありがとう。「1」
友人: 「2、3、4」
金田: (ここで長考に沈む。実は少し進んでから考えれば何とかなると思っていたのだが、その考えが甘かったことに気づく。結局…)
負けました(涙)
以下、私の考えた内容です。
「21」を相手に言わせれば良いので、自分が「20」を言えば良いことになります。
ということはその前の段階で「16」を言えば相手が1個でも2個でも3個でも自分の個数を調整して「20」にすることが可能です。
だからこのゲームの必勝法は「16」を言うことであると考えました。
ここまでが見えたので、再度勝負を挑んだのですが、まだ先がありました。
当たり前ですが、「16」を言う前の段階で「12」を言えば、必ず「16」を言えます。
そしてその前は「8」さらにその前は「4」となり、これは後手必勝を意味します。
ここまでを理解して友人の巧妙な手口に気がつきました。
最初は必勝のはずの後手を相手に譲ります。
しかし、一瞬で必勝法までたどりつくことはほぼありませんから、「4」を逃した時点で負けが確定します。
2回目は後手なので必勝です。
仮にその後も勝ち続けたければ「29」ゲームにしたり、一度に4つまで数字が言えるようにルールを変えれば大抵の人はすぐには対応できないでしょう。
まんまとやられた苦い思い出です。
では少し算数的にこのゲームを考えてみましょう。
実は入試問題でも出題例があります。
まず、2人で合計何個の数字を言えるかというと、
(1個、1個)の2個から(3個、3個)の6個までです。
この中で後手が必ず言うことができる個数は4個だけです。
(1+3=4,2+2=4,3+1=4)
次に最終的にいくつを言えば勝てるかというと
21-1=20
で、これは4で割り切れる数です。
ですから先に「4」を言ったほうが勝ちとなり、結論は「後手必勝」となります。
では「22ゲーム」ならどうかというと、
22-1=21
なので、これは4で割ると1余る数です。
なので「1」を言ったほうが勝ち、すなわち「先手必勝」となります。
数字がランダムな場合、先手必勝の確率のほうが高いです。
また一度に言える数字が多くなると先手必勝になる確率がさらに上がります。
整理します。
Nゲーム(Nを言ったら負け)
一度にA個まで言えるとすると、
(N-1)を(A+1)で割ったときのあまりを調べる。
①割り切れれば「後手必勝」→(A+1)を確保し、以後(A+1)ずつ増やしていき(N-1)を言えば勝ち。②B余れば「先手必勝」→Bを確保し、以後(A+1)ずつ増やしていき(N-1)を言えば勝ち。
最後にこのゲームでの勝率を上げる方法を考えます。
普通にやっても最初の何回かは勝てるはずですが、勘の鋭い人は少なくとも自分がハメられていることには気づきます。
なので、相手にいかに勝てそうな感覚を持ってもらうかが腕の見せ所となります。
1度に言える個数は3個に固定するとして、相手に「21」を好きな数字に変更してもらうのが現実的です。
その代わり「先手」か「後手」をこちらが選べば必勝です。
また、相手に先手を譲るかわりにこちらが数字を変えるのも手です。
「29」や「33」のような「4で割って1あまる数」を選べば「後手必勝」となります。
どちらにせよ、あまり大勝するとケンカになるかもしれませんから、ほどほどにしてくださいね。
具体的な算数の問題に関するご質問など、お子様の中学受験に関してお困りの点がございましたら、こちらのフォームからご質問を承ります。
お寄せいただいたご質問へは当ブログ上にてご回答させていただきます。
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の基本2題図形の移動 推理・論理
難易度★★☆☆☆
- 〈図1〉は、中心がOで半径が3cmの円から、AOBを取り除いた図形Pを表しています。
AOは円の一部であり、その中心はBです。
同じく、BOも円の一部であり、その中心はAです。
また、∠AOBは60°です。
〈図2〉は、図形Pと、1辺の長さが21.7cmの正三角形を表しています。
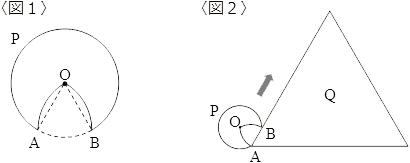
いま、図形Pが〈図2〉の矢印の方向にすべらないように転がって、正三角形Qのまわりを1周して元の位置に戻るとき、中心Oが動いた距離は何cmですか。
ただし、円周率は3.14とします。 - 「111ゲーム(111を言ったら負け)」
をA、B、C、Dの4人でやることになりました。
1度に言える個数は1個から3個です。
A → B → C → D → A → B → …
の順番で数字を言っていくことが決まっています。
実はAとBが仲間で、何とかしてCを負かそうと考えています。
そして必勝法を以下のように考えました。
最初Aは(あ)個の数字を言い、Bは(い)個の数字を言う。
その後Bが(う)で割って(え)余る数を言えるようにAが調整する。
具体的には(お)から、直前にCとDが言った数字の個数の合計を引き、
それが(か)よりも小さければ(き)個、
(か)よりも大きければ(く)個の数字を言えばよい。
このようにしていけばBは必ず「110」を言うことができるので、Cを負かすことができる。
に当てはまる数字を求めてください。
解答が表示されます
- 75.36cm
- (あ)3(い)3(う)8(え)6
(お)8(か)4(き)3(く)1













