VOL.73【ミニ講座】(11)比の式を立てる (12)グラフ
皆さん、“生金田”を見るチャンスがやってきました!!
8月27日は横浜、8月29日は目白で「中学入試ガイダンス2018」が行われます。
そこで、「これからの時期に必要な対策」と題して対談形式でお話をさせていただくことになりました。
夏期講習が終った後の指針をしっかりと示し、特に秋以降は志望校対策がメインとなるので、そのあたりをお伝えできればと思います。
皆さんのお役に立てるようなお話ができるようしっかり準備します。
ライブなので、ブログには書けないような内容も飛び出すかもしれません。
皆さんにお会いできることを楽しみにしています。
それでは「ミニ講座」です。
◎【ミニ講座】(11)比の式を立てる
「倍数算」の解法は
①「和が一定」
なのか
②「差が一定」
なのかで異なります。
①は1本の線分図を描き全体の比を合わせれば解決し、
②は差が残るように2本の線分図を描き差の部分の比を合わせれば解決します。
「倍数算」の「上級分野」とも言える「倍数変化算」の解法は色々ありますが、一番簡明なのは「比の式を立てる」ことでしょう。
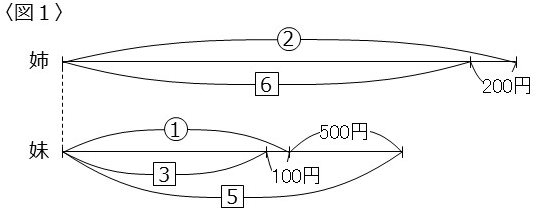
<問題>
はじめ姉と妹の所持金の比は2:1でしたが、姉が200円使い、妹が500円もらったので、6:5になりました。はじめに姉はいくら持っていましたか。
<比の式を立てる解法>
②-200:①+500=6:5
(②-200)×5=(①+500)×6
⑩-1000=⑥+3000
④=4000
②=2000(円) …(答)
<別解>
もしも妹が100円使ったとしたら姉と妹の所持金の比は2:1のまま。その時の所持金を姉⑥、妹③とすると、実際は妹が100円使わずに500円もらったので、それは⑤である。⑤と③の差の②が、100円と500円の和である600円なので
②=600円
⑥=1800円
1800+200=2000(円) …(答)
「算数」を学ぶ上で、複雑なものや面倒なものに挑むことは「力」をつけるという観点からは必ず必要だと思いますが、実際に試験当日に問題を解く際は、なるべくわかりやすく解きたいということがあります。
そこで、普段の勉強はどうすれば良いかという問題が生じます。
試験当日に使うと思われる解法だけやっていると、「粘り」や「思考力」が養われないかもしれません。
逆に、当日は使わないと思われる面倒な解法ばかりでは、本番に不安が残ります。
何事もバランスが大切ですが、そのバランス調整こそ我々の腕の見せ所です。
「倍数変化算」の場合、正解率が下がる分野なので、まずは正解できるようにすることが第一だと思います。
ですから、ほとんどの生徒さんに対して「比の式を立てる」ように指示しています。
問題文の言っていることを素直に式にすれば「比の式」が完成します。
ですから、「比の式」が解ければ、ほぼ正解できるようになります。
また、この「比の式を立てる解法」は応用範囲が広いです。
様々な文章題で使うことができるので、まだマスターしていない受験生は、夏休み中に自分のものにすると良いと思います。
「比の式をたてる解法」をマスターした後に別解として他の解法を学ぶことが多いです。
特に、「もし同じ割合で減ったら(増えたら)」という発想はよく使うので、1度はやっておきたいですね。
「比の式を立てる」ことが有力なのはわかったのですが、ひとつ困ったことが起きました。
それは「比の式を立てる」ことで普通の倍数算も解けてしまうということです。
実際、一部の塾ではそのような指導をしているところもあるようです。
同じ解法で解けるならそのほうが良いという考え方もあるでしょう。
しかし、「比の式を立てる解法」というのは「方程式」で解くのと実質は同じです。
前にも書きましたが、全ての問題を「方程式」で解くのは「中学受験」では得策ではありません。
もちろん、「方程式」を扱えるということは武器にはなります。
全部「方程式」で解くことで「算数的な発想」を学ばないことが問題だと思うのです。
そこで、私の結論です。
「倍数算」は「和一定」と「差一定」で線分図が異なる等、「算数的発想」を学ぶには最適な分野です。
ただし、「倍数変化算」はまず正解するということを重視し「比の式を立てる」解法を学びます。
「比の式を立てる解法」は文章題では特に威力を発揮するので、マスターしておけば大きな武器になります。
ただし乱用は禁止です。
やはり線分図等を描いてそれを見ながら解くのが文章題を解く際の基本です。
◎【ミニ講座】(12)グラフ
算数で扱うグラフには様々なものがあります。
「棒グラフ」、「折れ線グラフ」、「円グラフ」、「進行グラフ」、・・・
それらは全て、複数のデータを視覚化していると言えるでしょう。
もう少し踏み込んで言えば、数量を図形化しているということでしょうか。
これはとても大きなことです。
今回はそのことについて説明をしたいと思います。
まず、算数の分野は大きく分けて「数量」と「図形」の2つの分野からなります。
「数の性質」や「規則性」は「数量」、「平面図形」や「立体図形」は当たり前ですが「図形」の分野です。
また、「図形の規則性」のようにどちらの分野にも関係するものもあります。
私がいつも言っているのは「数量⇔図形」が大切であるということです。
「数量」と「図形」の間を自由自在に行き来できるのが理想なのです。
例えば「つるかめ算の問題」を解くとしましょう。
「つるかめ算」は数量の分野ですが、面積図を描いて解くケースも結構あります。
長方形を2つ描いた時点でそれは「図形」です。
そしてその「図形の面積」に着目して問題を解くわけです。
この例では、「数量」⇒「図形」⇒「数量」という流れが感じられたのではないでしょうか。
もちろん最初から最後まで「数量」で押し通すこともできます。
ただ「図形」で考えることには様々なメリットがあるので、問題が複雑であればあるほど「図形」を経由して解きたくなるのです。
以下、「図形」で解くことのメリットを挙げます。
- 視覚的にとらえることができるのでわかり易い。
- 「計算量」を減らすことが可能。
- おおよその大きさや、範囲が自然とわかる。
- 対称性や拡大・縮小等図形的性質を活かして解くことができる。
- 直観的に答を出すことが可能。
その他にも色々ありそうですが、良いことずくめであると言っても良いでしょう。
私は、算数ができるようになるコツは、極力「図形」を経由して解くことにあると考えています。
※勉強のコツは「図形」<「数量」である言わば例外的なケースをきちんと認識し、そこは「数量」で押せるようにしておくことだと思います。
そこで、「グラフ」です。
本来は数量で与えられるものが「グラフ」で表現されることによって「図形」になるのです。
私が良く生徒に言うのは、「グラフを描いてしまえばそれはもう図形問題」であり、「図形問題は図形的性質を利用して解く」ということです。
「速さ」の問題で「2本のグラフ」が交差していれば『「砂時計型の相似」を使って解け』と言っているようなものなのです。
もちろん、「旅人算」を使って解けるならそれでもかまいませんが、「相似」を利用するよりも面倒になることがほとんどでしょう。
「グラフ」を利用して問題を解くことは「試験本番」でもそのようにすべきですし、グラフから図形的な性質を探し出し、それを基にしてして答を出すというやり方は「思考力」を鍛える要素もありますから、普段からそのような取り組み方をすることがおすすめになります。
最後に2020年の大学入試改革について一言。
「センター試験」が「大学入試共通テスト」になるわけですが、「数学」と「国語」では従来のマークシート式に加え記述問題が出題されるとのことです。
また、「十分な知識をもとにした思考力・判断力・表現力を重視する」 ということらしく、単なる丸暗記では全く太刀打ちできないテストになるのではないでしょうか。
「グラフ」から情報を読み取るような問題も出題が予想され(特に理科)、今のうちから「グラフ」に強くなっておくことは、「大学入試共通テスト」でも大いに活かされると思います。
「今の頑張り」は「今の自分」だけでなく「将来の自分」にも良い影響を与えるのですね。
具体的な算数の問題に関するご質問など、お子様の中学受験に関してお困りの点がございましたら、こちらのフォームからご質問を承ります。
お寄せいただいたご質問へは当ブログ上にてご回答させていただきます。
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の基本2題文章題 表とグラフ
難易度★★☆☆☆
- 最初、姉と妹の所持金の比は2:5でした。
妹がおこづかいを200円もらい、姉が700円使った後、姉が所持金の9分の1を妹にあげたところ、妹と姉の所持金の比は7:8になりました。
最初の姉の所持金を求めてください。 - 〈図1〉の四角形ABCDは1辺が40cmの正方形で、ADとEFは平行です。
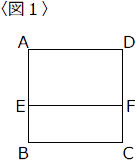 点PはAD間を、点QはEF間を、点RはBC間を、それぞれ一定の速さで何回も往復します。
点PはAD間を、点QはEF間を、点RはBC間を、それぞれ一定の速さで何回も往復します。
点PはAを、点RはBを同時に動き出し、それから遅れて点QがFから動き出します。
また、点Qは点Pより速く、点Rより遅いことがわかっています。
〈表1〉は、点Pが動き出してからの時間と、APとEQの長さの差をあらわしたものです。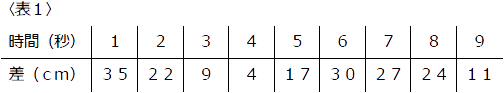 〈グラフ1〉は点RがBから動き出してからの時間と、BC間のどこに位置するのかの関係をあらわしたグラフです。
〈グラフ1〉は点RがBから動き出してからの時間と、BC間のどこに位置するのかの関係をあらわしたグラフです。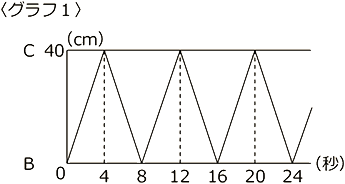 点Pと点Rが動き出してから、3点P、Q、Rが同じ⽅向に進み、かつ、その間、同
点Pと点Rが動き出してから、3点P、Q、Rが同じ⽅向に進み、かつ、その間、同
⼀直線上にならんでいるということがありました。
そのようなことが初めて起こるのは、点Pと点Rが出発してから何秒後から何秒後ま
での間ですか。
また、〈図1〉のFCの⻑さは何cmですか。
解答が表示されます













