VOL.71【ミニ講座】（７）重複組合せ　（８）ハップス・ギュルダンの定理

今回はいきなり「ミニ講座」からです。
なぜかって？
それは内容が盛りだくさんだからです！
決して暑さで手抜きしているわけではありません。

◎【ミニ講座】（７）　重複組合せ
昔、次のようなクイズを解いたことがあります。

Ｑ：ある村の農夫が亡くなった。彼は遺言を残しており、それは以下のようなものであった。
『私の全財産の １２ を長男に、 １３ を次男に、 １９ を三男に贈る。』
その農夫の全財産は卵を産む雌鳥１７羽だけだった。
困ったのは残された３人の息子たちで、 12 や 13 にしようにも割り切れない。
どうしたらよいか悩んでいたところ、ある賢者が現れ、見事に誰も損することなくこの問題を解決したという。
賢者はどのような解決策をとったのだろうか。

Ａ：賢者は次のような策を示した。
私がこの雌鳥１羽を差し上げましょう。
そうすれば１８羽になり、２でも３でも９でも割り切れます。
計算すると長男は９羽、次男は６羽、三男は２羽ですね。
これでうまくいきました。
あれ、１羽余ってますね。
ではこの１羽は私が返してもらいましょう。

そもそも遺言がおかしくて、足して1にならないのですが（笑）
それはともかく、なかなかうまい解決策で、「算数でこれが使えればよいなぁ」なんて考えていました。
実は「重複組合せ」でこの賢者のやり方が使えます。
問題を解きながら説明しましょう。

＜問題＞
みかん５個をＡ、Ｂ、Ｃ、Ｄの４人に分ける分け方は何通りありますか。
ただし、もらわない人がいてもよいものとします。

＜解決策＞
金田賢者 ：
もらわない人がいるとかわいそうなので、私がみかん４個を提供します。
そうすれば、皆、最低１個はもらえます。
９個のみかんを４人に分けるのですが、
これは９個のものに対して、３つの仕切りを入れるということなので、
８個の中から３個を選ぶ組合せになります。
よって 8×7×63×2×1 ＝５６（通り）　…（答）
あっ、そう言えばさっきのみかん、やっぱり気が変わったので返してくださいね。
一人１個ずつ、よろしくおねがいしまーす。

◎【ミニ講座】（８）　ハップス・ギュルダンの定理
算数にも「裏ワザ」というものが存在します。
私はこの「裏ワザ」はあまり好きではないのですが、この「ハップス・ギュルダンの定理」に関しては積極的に活用すべきであると認めざるを得ません。
実際の入試問題でも、導入部にこの定理があり、ドーナッツ型の体積を求めるようなものを見たことがあります。
「ハップス・ギュルダンの定理」をざっくり説明すると、平面を回転軸のまわりに1回転させる場合、回転させる平面の重心が動いた距離にその平面の
① 面積をかければ「体積」
② 周をかければ「表面積」
が求められるというものです。
ただし、回転軸とその平面が重なってはいけません。

この定理が実に便利です。
特に、線対称かつその対称軸が回転軸と平行な場合、あっという間に答が出ます。
例えば、回転軸と回転させる平面が離れていて、その平面が「等脚台形」なんていうのが最高ですね。
このケースは「裏ワザ」を使わないとかなり大変なので、答を出すだけならこの「裏ワザ」の使用がほぼ絶対といえるかもしれません。
さて、今回のメインテーマは
『「線対称ではない図形」でこの「裏ワザ」が使えないか？』
です。
結論から言うと「三角形なら使える」ということになります。
まず、重心とは何かを確認しましょう。
算数（数学）的には
「三角形の３つの中線（頂点から対辺の中点に引いた線分）の交点」
ということになります。
そして頂点から重心までと重心から中点までの比は２：１になることが知られています。
つまり、三角形の重心がどこにあるかは求められるということです。
そうすると回転軸から重心までの距離も求められる、だから「裏ワザ」が使える、となるわけです。

では具体的に見ていきましょう。

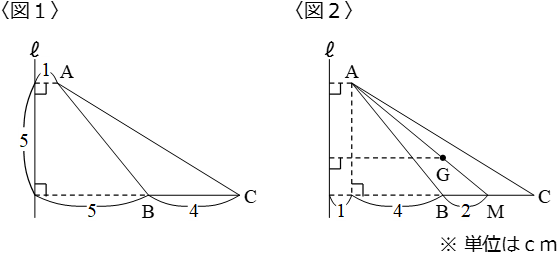
〈図１〉で三角形ＡＢＣを直線ℓを回転軸として１回転したときの体積を考えます。
ただし円周率は３．１４とします。
〈図２〉はＢＣの中点をＭとし、ＡＭを結ぶとその線分上に重心Ｇがあるようすをあらわしています。また、ＡＧ：ＧＭは２：１です。
軸ℓからＧまでの距離ですが、〈図２〉より
１＋（４＋２）× ２２＋１＝５（ｃｍ）
と求められます。
よって求める答は
４×５÷２×５×２×３．１４＝３１４（ｃｍ^２）　…（答）
あっさり解けてしまいました。
これが「ハップス・ギュルダンの定理」の威力です。
ただし、この定理は高校の数学までいっても学校で習うことはないのであくまで「裏ワザ」です。
答を出すだけなら本当に素晴らしいのですが、途中の考え方や計算式を書く場合の使用は「自己責任」ということになってしまいます。
そこだけが非常に残念ですが、とにかく答を出すだけなら威力抜群なので、マスターすることをおすすめします。

具体的な算数の問題に関するご質問など、お子様の中学受験に関してお困りの点がございましたら、こちらのフォームからご質問を承ります。
お寄せいただいたご質問へは当ブログ上にてご回答させていただきます。