VOL.66平面図形(2)
日本は地震が多い国です。
海に囲まれているので津波の心配もあります。
あまり心配し過ぎるのもよくないのでしょうが、日ごろからしっかりとした対策を考えておきたいですね。
私は「津波がおきたら高いところまで走る」、「火事になったら煙を吸わないように態勢を低くして外に逃げる」なんてことを頭の中でシュミレートしたりしています。
ほかにも防災グッツや非常食を準備したりもしています。
受験も何が起きるかわからないので、様々な状況に対応できるようシュミレートしておくと良いかもしれません。
今回はレギュラーになりつつあるE君が来てくれました。
なにか報告があるようです。
E君金田先生、こんにちは。
金田こんにちは。E君はいつも元気ですね。
E君ありがとうございます。
今日は僕が作ったノートを見てもらいにきました。
金田ほう、どんなノートなんですか。
E君「平面図形攻略ノート」です。
金田なにか凄そうな名前ですね。では早速見せてもらいましょうか。
E君どうぞ、これです。
―――E君はノートを手渡した
金田なるほど。
「平面図形」の問題の解法のポイントをE君が自分なりにまとめたノートですね。
しかも、何回も復習したんですね、所々傷んでいます。
ノートは書いて終わりではほとんど意味がありません。
E君のように見直しをして内容を自分のものにすることが肝心です。
最初は「面積の公式」ですね。しっかりとよくまとめられています。
E君ありがとうございます。
公式が完璧ではなかったので、ノートにまとめて覚えました。
金田「面積の公式」のあとは「角度」ですね。
中学の数学で習う「同位角」や「錯角」の文字が目に入ります。
受験とは直接関係ないかもしれませんが、高級な言葉を自分のものにすることはとても良いことです。
E君の意識の高さには感心させられます。
E君えへへ、それほどでもないです。
金田大切なポイントがしっかりおさえられていますね。
難点を挙げるとすれば、少し遠回りしているケースがあることでしょうか。
最終的には答がでれば良いのですが、受験は時間とのたたかいでもあるので「シンプルが一番」です。
角度の問題に関しては、別解も重要ですが、なるべくスマートに求められる道筋を目指すと良いと思います。
E君はい、頑張ります。
次の「面積比」のところはちょっと自信があります。
金田そうですね、典型的な問題の解法がコンパクトにまとめられています。
どこの面積を基準にするかが重要なのですが、とてもわかりやすく書いてありますね。
E君このノートにまとめてからかなり自信が持てるようになりました。
この間の模試では会場に持っていき、直前まで確認してました。
金田以前なら「面積比」を求めるのに「線分比」を使うか「相似比」を使うか混同していたところがありましたが、ずいぶんスッキリしたようですね。
E君はい、今までみたいにやさしい問題での取りこぼしがずいぶん減りました。
金田それこそが「実力」がついてきたことの証です。
E君なんか嬉しいなぁ。ますますやる気がわいてきました。
金田いよいよE君も「算数」ができる側の世界に引っ越してきましたかな。
最後は「相似」ですね。
E君が初登場だったVOL.58のときのテーマでした。
E君あの頃はよくわかってなかったというか・・・。
金田小学生の成長力は凄いですから、今のE君はあの頃とは別人と言って良いかもしれません。
E君自分でもそんな気がします。
金田VOL.58のときにやった「平行」と「直角」が関係する「相似」以外に、「裏返し」の相似がまとめられていますね。
「相似」の中では比較的難易度が高いテーマですが、そこまで踏み込んでいける積極性は素晴らしいです。
全体に目を通しましたが、余裕で合格点に達しています。
良いものを見せてもらいました。E君の努力の結晶ですね。
このノートの完成度はかなり高いですが、今後はどうしていくつもりですか。
E君次は「立体図形攻略ノート」を作るつもりです。
金田そうですか。それは楽しみです。
完成したらまた見せにきてください。
E君はい。よろしくお願いします。
今日はどうもありがとうございました。
金田本当に別人だな。何か秘密があるかも・・・(独り言)
<ポイント>
- 「平面図形」は「形」と「解法(考え方)」をまとめることが有効。
- まとめる際はなるべく「シンプルに」ということを心掛ける。そしてそれを何回も見て、自分のものにする。
- 小学生は「一夜明けたら別人」ということもあるぐらい成長がはやい。
可能性を信じて努力した者は、ご褒美がもらえる。
具体的な算数の問題に関するご質問など、お子様の中学受験に関してお困りの点がございましたら、こちらのフォームからご質問を承ります。
お寄せいただいたご質問へは当ブログ上にてご回答させていただきます。
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の1題平面図形
平面図形の問題はVOL.8、VOL.16、VOL.22、VOL.41、VOL.50、VOL.58にもあります。
難易度★★★☆☆
〈図1〉のように、1辺の長さが30cmの正三角形ABCがあり、
点Dは辺ACの中点です。
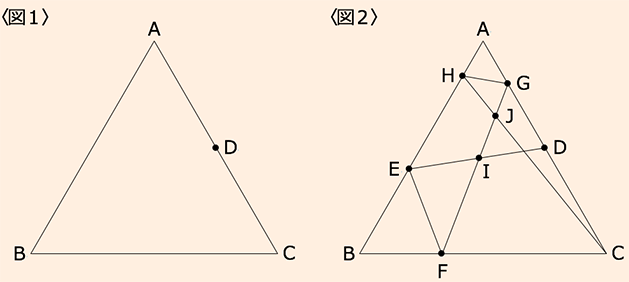
今、辺AB上に点Eと点H、辺BC上に点F、辺AC上に点Gをそれぞれとり、
D→E→F→G→H→Cの順に直線で結び、
この長さが最も短くなるように点Eから点Hの位置を決めます。
〈図2〉はD、E、F、G、H、Cを結んだ様子です。
(1) EHの長さを求めてください。
(2) 〈図2〉のFI:IJ:JGを求めてください。
解答が表示されます













