VOL.336【夏休み特集】 ― 本格的な勉強 ―
今回はお約束通り「本格的な勉強」について書きます。
そもそも「本格的」とはどういったものかというと,『本来の格式や性質が整っている・すっかりそのような様』という2つの意味で使います。
「本格的な受験勉強」というと,『本腰を入れて本気で取り組む受験勉強』といった後者の意味で使われることが多いでしょうか。前回の流れで最後に書いた「本格的な勉強」の意味は前者で,『付け焼刃ではない本物の勉強』という意味で使いました。
前回書いた4つの項目全てでうまくいくような勉強が「本格的な勉強」であると考えられます。
4つの項目を改めて記載します。
①記憶の定着
②解法の検索
③知識を実際に解くことに活かす(力の養成)
④応用力を身につける
受験生の皆さんには,夏休みに上の①から④全てがうまくいくような勉強を目指して欲しいのです。気をつけるべきことを挙げることによって,具体的なやり方をイメージしていただければと思います。
(1)基本から積み上げる
「算数は積み重ねの科目」といったことがよく言われます。前にやったことがわかっていることが前提で次のことを学ぶタイプの科目ですね。一番下の土台に数の概念や計算といったものがあり,その上に各単元を積み上げていくようなイメージです。さらに言えば各単元も最終的には一体となり,自分の算数といったものが形成されることになります。
受験勉強はその最終形を志望校の出題傾向に合せてデザインし,本番までに完成させることを目指すわけです。

大切なのは主に3つです。
・下から積み上げるので,特に大切なのは土台の部分。計算力は絶対必要。基礎が抜けているということは許されない。
・各単元を高く積み過ぎると崩れてしまう可能性が高い。理想は「ミルクレープ」。全体を薄く確実に学び,それを何層も重ねて強固なものをつくっていく。
・最終的なデザインが志望校で出題されるものとほど遠いと効率が悪い。なるべくデザインを近付けたい。
穴がなく,きれいな形を目指して欲しいと思います。
(2)塾に振り回されない
やったことをきちんと定着させるには復習の時間が必要です。この時間がどれ位必要かについては個人差があります。
ほとんど時間が必要ない受験生は良いのですが,じっくりとやらなければならないタイプの受験生は時間の余裕が不可欠です。受講生一律の講義や宿題は時間に余裕のない者にとっては負担が重過ぎるかもしれません。その場合は講義や宿題を間引くといった決断も必要なのですが,現実的には難しいと思われます。
個別授業ならそのような心配はいらないのですが…
(3)理解→記憶→運用
算数はこの3つのプロセスを経て本物になります。
なぜそうなるのかを理解することがはじめの一歩です。きちんとした理解があればすんなりと記憶することが可能でしょうし,忘れそうになった時に根本に立ち返って思い出すことも可能でしょう。そのようなことを繰り返していけば記憶は盤石なものとなります。
問題の解き方を覚えたらそれを実際に使うこともセットでやらなければなりません。
そして,日頃から1つの解法を使える範囲を広げることを意識しておけば,応用力が無いと悩むことも少なくなると思われます。
解法を思い出すタイミングも重要で
・直後
・1週間後
・1カ月後
・3カ月後
上のどのタイミングでも大丈夫なら記憶が定着したとみなして良いと思います。
これらの確認に最適なのが「基本書の繰り返し学習」で,そのことについては本ブログで何回か書いてきました。
できれば夏休み期間もやって欲しいと思います。2回転できれば理想的です。
(4)頭を使う
自分の頭を使って考えるにはどうすればよいでしょうか。
よく難問を前にウンウンうなりながら固まっているシーンを目にしますが,これは無意味なことが多いです。
頭を使うためにはまず手を動かすことです。「わからない」と嘆く前にまずわかっていることを「書いてみる」。そして,それを少しずつで良いので膨らませていく。このような姿勢で問題に対峙すれば頭が使えるようになっていくものと思われます。
その際,「積極的」「楽しむ」「リラックス」「自信を持つ」といった精神状態で臨むことができれば算数はドンドンできるようになっていきますよ。ただし,時間無制限というわけにはいきませんから,時間の管理をお忘れなく。できれば我々指導者が側についているのが理想ですが,そうでない場合はあらかじめ制限時間を設けておく必要はあるでしょう。
また,ぜひやって欲しいのが「一日一膳」ならぬ「一日一計算の工夫」です。
計算を何も考えずにやるのではなく,全体を俯瞰し何かないか考えてみるということをやって欲しいのです。その結果として一日に一題で良いので,計算の工夫の実績を作って欲しいと思います。
夏休みは以上のようなことに気をつけながら勉強すれば本格派の仲間入りです。気が付けば「本格的な勉強」ができていた,となることを期待しています。
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の1題点の移動
難易度★★★★☆
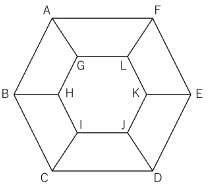
〈図1〉は1辺が6cmの正六角形ABCDEFと1辺が3cmの正六角形GHIJKLの頂点同士を長さ3cmの線分6本で結んだ図形です。
〈図1〉
2つの点,点P,点Qが〈図1〉の正六角形の辺上を動きます。点Pは正六角形ABCDEFの頂点Aから反時計回りに毎秒3cmの速さで,点Qは正六角形GHIJKLを頂点Gから反時計回りに毎秒1cmの速さで動きます。
今,点Pと点Qが同時に動き出し,点Pが頂点Aに,点Qが頂点Gに同時に到着して止まりました。
2つの点が出発してからX秒後の,2つの点の〈図1〉の線上での最短距離を〈X〉とあらわすことにします。
〈図2〉に示すように,例えば,X=2のときの〈2〉は4cmです。
〈図2〉

(1)Xが2~4の範囲の〈X〉の最大値を求めてください。
(2)〈X〉の最大値はいくつですか。さらに,その時のXの値を全て答えてください。
(3)〈X〉=13cmとなるXをすべて答えてください。
解答が表示されます
(1) Xが2~4の範囲の〈X〉の最大値 7.5cm
(2)〈X〉の最大値 13.5cm そのときのX 17.25,18.75
(3) 15.5,17,17.5,18.5,19,20.5













