VOL.161【入試問題を解いての感想】 -(16)女子学院-
この企画は書いている私にとっても面白く、まだまだ取り上げたい学校が沢山あるのですが、そろそろ終わりにする時期かなとも思っています。
そうなると、人気のある学校を優先しなければ皆さんに怒られてしまうかもしれませんね。
というわけで今回は「女子学院」です。
女子御三家の一角であり、自由な校風で人気の名門校です。
入試問題はというと「多問即答型」という評価が定着しているようです。
今年は一体どんな問題だったのでしょう。
◎女子学院
1.小問集合
(1)小数・分数混合の逆算でした。
ここでも「0.325」が出てきましたね。
3 8 ではなく 13 40 です。
(2)ひし形の面積を求める問題でした。
30°・75°・75°の二等辺三角形の面積は常識にしておかなければなりません。
(3)正方形内部に5本の線を入れ角度を求める問題でした。
ここでも上の二等辺三角形が出てきたので、少し偏りを感じました。
アは知識でOK、イは二等辺三角形の発見がカギでした。
(4)割引を考慮する必要がある消去算でした。
一瞬袋の値段を取られるのかなと思いましたがそれはありませんでした。
来年は数が増えると袋代が別途かかる問題もあるかもしれませんね。
(5)最小公倍数を利用する日暦算の問題でした。
本校の受験生ならあっさりクリアしたい問題だったと思います。
1を足すのを忘れずに!
(6)直角三角形の角度を見分ける問題でした。
本来なら私からのアドバイスは
「印をつけろ」
ですが、解答の方法が
「〇か×を入れる」
ですので、完全に取らせてくれる問題でした。
2.直角三角形に内接する正方形、さらにその正方形に内接するおうぎ形に関する問題
(1)はよくある問題でした。
ただし答が分母が17の分数だったので少し厄介だったのかなと思いきや、(2)でその分母が消えてしまうというハイセンスな問題でした。
この数の扱いはお見事と感心しました。
3.算数で習う事柄について、言葉の知識を問う問題
数学経験者にとっては当たり前のことばかりでしたが、小学生がこれらをいきなりきかれて即答できたのかどうか。
意外と差がついた問題だったかもしれません。
4.立体上の点の動きにグラフを絡めた問題
一見複雑でつかみどころがないのですが、「辺の長さが2倍のところは速さが2倍」の意味することに気付けば、残る問題はおうぎ形の弧の部分の速さだけということになります。
この手の問題で怖いのが計算ミスですが、本校の受験生はそのあたりの備えはしっかりしていたでしょう。
5.4つの数字の和が常に同じ値となるように数字を入れる問題
この問題は面白かったです。後ろの「今週の1題」は本問の応用問題にしました。
本校のように時間的な余裕がない場合、運の要素が強くなってしまうのが少しもったいなかったかとも思いますが、十分楽しませていただきました。
6.少し複雑な流水算-2人が出会った時刻を求める問題
(1)を解く過程で速さが全て明らかになるので、表にまとめておくと良いでしょう。
(2)はこの手の問題を解く際の「定石」である「グラフの利用」が得策です。
戦略的には、5.をあまり深追いせずに、6.をしっかり取り切るのが良かった可能性が高かったでしょう。
面白い問題が多く解いていて楽しかったのですが、ちょっと待てと思いました。
これは時間的にかなり厳しいぞ!
もともと時間を考えると大変な問題だったのですが、それに加え「思考力」のようなものまで要求されているのですから、私としては「さらにやり甲斐のある学校になったなぁ」
というのが正直な感想です。
来年も同じような問題が出題されることを密かに期待しているのでありました。
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の1題整数
難易度★★★☆☆
下の5×5マスの表に数字を入れます。
完成した表に以下の<ルール>で数に〇をつけます。
<ルール>
①1つの数字を選び〇をつけ、その数と同じ行、同じ列に並んでいる印のついていない数すべてに×をつける。
②印のついていない残りの数の1つに〇をつけ、その数と同じ行、同じ列に並んでいる印のついていない数すべてに×をつける。
③さらに印のついていない残りの数の1つに〇をつけ、その数と同じ行、同じ列に並んでいる印のついていない数すべてに×をつける。
④もう一度②を行い、残った数に〇をつける。
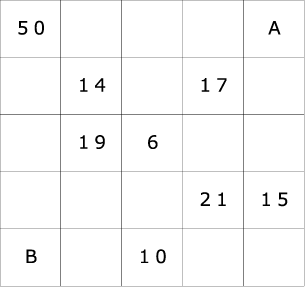
この表の一部は上のように整数が入っています。
そして、どこを選んで〇をつけていっても、①から④の作業をした後に〇のついた数の和がいつでも同じになることがわかりました。
また、マスに入る数字はどれも異なり、A<Bです。
(1)①から④の作業をした後に〇のついた数は全部で何個ありますか。
また、それらの和はいくつですか。
(2)5×5の表を完成させてください。
解答が表示されます
(2)