VOL.129【合格へのシナリオ】 -過去問演習の重要性-
前回、受験校を決めましょうという話をしました。
そして、その学校の過去問をやっていくのですが、色々と迷うことがあるかもしれません。
具体的には
(ア)いつから始めるのか。
(イ)どの学校からやるか。
(ウ)何年分(何回分)やるか。また、その順番は。
(エ)何回やるか。
といったことを全て決めなければなりません。
「過去問演習」によってもたらされる効果はいくつもありますが、代表的なものを挙げておきます。
(1)出題傾向を知ることができる。
(2)難易度を感じることができる。
(3)出題形式に慣れることができる。
(4)合格可能性をはかることができる。
よって、(1)~(4)のどの効果を重要視するかによって(ア)~(エ)が変わってくると考えることができます。
ですから、どこを受けるかということや、本人の実力等全てを加味しなければならないので、(ア)~(エ)の答は人それぞれとしか言いようがありません。
具体例を挙げます。
| (ア) | (イ) | (ウ) | (エ) | |
|---|---|---|---|---|
| A校 (第一志望) |
夏休みの終わりに1回やった。 12月から1月にかけて集中的にやった。 |
4番 | 10年分 古いものから |
2回 (記述に慣れるため) |
| B校 (第二志望) |
9月に1回やったが3割しか取れなかった。 11月に入ってから再開した。 |
3番 | 3年(6回)分 古いものから |
1回 |
| C校 (第三志望) |
10月後半から。 | 2番 | 3回分 新しいものから |
1回 |
| D校 (押さえ) |
10月前半から。 | 1番 | 2回分 新しいものから |
1回 |
(1)と(2)に関しては早い時期にやった方が良く、(4)は遅い時期の方が精度が高くなります。
(3)に関しては時期よりも慣れるかどうかが大切で、回数の問題です。
それらを何とかうまくやりくりしたというのが上の表になります。
<ポイント1> 早めに傾向や難易度はつかんでおく
A校とB校は早めの時期に1回やっています。
このことによって、普段の学習の広さと深さの調整をすることができます。
<ポイント2> 難易度が低い学校から始める
受験勉強の最終目標は「合格点を取れる」という自信を身に着けることとも言えるので、まずは取りやすいところから始めるのがセオリーです。
<ポイント3> 重要度が高いところの回数を多くする
当たり前ですが、回数を増やしたほうが得るものが多くなります。
ただし度を越えると見返りが小さくなってしまいますし、あまり古いものをやると傾向が変わっていることもあるので、何年分やるかは専門家のアドバイスに従うのが良いと思います。
<ポイント4> 算数は1回勝負
よく同じ問題を10回繰り返せば受かるといった話をききます。
資格試験か何かならわかりますが、中学入試の「算数」ということであるならば、うまくいかないケースが多いと思います。
同じ年度を10回繰り返すのであるならば、10年分1回ずつの方が明らかに効果的でしょうし、他校の過去問を解くことにすら劣る可能性があると思います。
上の表ではA校のみ記述の形式に慣れるために2回やっていますが、あとはすべて1回しかやっていません。
<ポイント5> 新しい年度から始めればいつでもやめることができる
A校とB校は古い年度から始め、C校とD校は新しい年度から始めているのには訳があります。
C校やD校はすでに合格レベルを超えている可能性もあり、そのことが確認できれば、あまり多くやる必要はありません。
その判断は新しい年度のほうが精度が高いので、新しい年度から始めているのです。
対してA校・B校は、早い時期にはまだ実力が足りていませんから、少し力をためて遅い時期のスタートになっています。
そして、(4)の精度を上げたいので、新しい年度は遅い時期にやっています。
以上、わかりやすい例を作ってみました。参考にしていただければと思います。
今回の「合格へのシナリオ」は「過去問演習」の実例です。
堀江君(仮名)は塾の成績はちょうど真ん中ぐらいで、秋になってもモチベーションが上がらないという生徒さんでした。
ご家庭はやる気があまり感じられないことに危機感を抱き、かなり心配していましたが、本人はマイペースを貫いていました。
私の方針は、「算数」の楽しさに目覚めてもらうことだったので、成績等もあまり気にせず、淡々と授業を進めていたのですが、気が付くと残り2ヵ月という時期にきていました。
そして、この時期に模試の偏差値も50を下回り、いよいよもって苦しくなってきました。
目標の偏差値は50後半でしたから、普通に考えると絶望的な状況だったかもしれません。
ただ、本人も私も純粋な算数の実力の部分に磨きをかけてきたという自負がありましたから、不思議と焦りのようなものはありませんでした。
私の中では「最後の仕上げ」で何とかなるという感触はありました。
ただ、問題があるとすると、その「仕上げ」に少し時間がかかってしまうかもしれないということでした。
幸いなことに、冬休み以降は十分な授業時間を確保していただいたので、じっくりと「最後の仕上げ」を行うことができました。
「最後の仕上げ」は「過去問演習」なのですが、特に「点数の取り方」にフォーカスをあてたものです。
堀江君と取り組んだのは主に以下の3つです。
①時間の管理
②自信度をメモる
③解答順や確かめについての約束事
まず①の時間の管理ですが、50分を3つに分けました。
・25分…全体に目を通した上で、50%正解することを目標とする
・15分…後回しにした問題の中で解けそうな問題や、不安がある問題を確実に正解にしていく
・10分…見直し等を含めた最終チェック
特に最初の25分が勝負で、ここはスピードに磨きをかけておかないとなかなか目標通りにはいきません。堀江君も最初のうちは苦戦しましたが、徐々に思い切りの良さ(出来そうもないものは飛ばして次に行く)が出てきたので、時間の管理はうまくいくようになりました。
②の自信度をメモることが一番効果が大きかったのです。
これは問題を解く度に「◎、〇、△、×」の記号をメモするだけなのですが、今回の戦略の肝になった部分です。
◎ … 絶対正解なので、以後見直しもしない。当然検算は済んでいる。
〇 … 正解だと思うが、検算の必要なしとまではいかない。
△ … とりあえず答えは出した、あるいは考え方はわかりそうだが、答えまではでていない。
× … わからない。
③の決め事は徹底しました。
Ⅰ.確かめはその都度やる。
逆算や文章題はその検算により◎にすることができる。
Ⅱ.解答順はまず得意分野からやる。
小問の「平面図形」→「立体図形」→「計算」→「文章題」→「数の性質」→「規則性」→「場合の数」
大問も小問と同様の順番
「図形」は解法が浮かばなければすぐ飛ばす
「規則性」で書き出しで解く場合は後回し
「場合の数」は明らかにすぐ解ける場合以外は飛ばす
Ⅲ.①の「15分」の時間帯は△を〇に変えることが一番価値が高いのでそれを優先する。
Ⅳ.最後の「10分」は〇を◎に変えるとともに、保留していた「書き出せばなんとかなる」ようなタイプの問題にチャレンジすることも可。
以上のような決め事を作り、過去問を目の前で解いてもらい、できているかどうかのチェックをその場で行いました。
最初(1月初め頃)は60%程度の点数だったのが、ある日(1月中旬)突然85%に跳ね上がりました。
そして、その後は満点こそありませんでしたが、85%以上をずっとキープすることができました。
結果はまるで受かって当然かのように
浅野中学合格!
「過去問演習」の効果が見事に出た生徒さんでした。自信を持つことは本当に大切だと実感させられました。
具体的な算数の問題に関するご質問など、お子様の中学受験に関してお困りの点がございましたら、こちらのフォームからご質問を承ります。
お寄せいただいたご質問へは当ブログ上にてご回答させていただきます。
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の1題分数
難易度★★☆☆☆
91937 269047 の約分をするとき、以下の手順を行うことにしました。
<手順>
①最初の分数の逆数をつくり、それを整数部分と分数部分に分けることで
B A = 1 M+ P N (M:整数部分、 P N :分数部分)
の形で表す。
②次に、 P N にも①と同じことを行う。
③さらに分数部分に同じことを繰り返し行い、分子が1になったら終了する。
④途中では約分はしない。
例えば、 45 51 は、
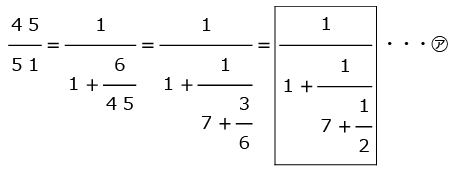
となります。
このときの 1 2 を最後の分数、
その一つ前の 3 6 を最後から二番目の分数と呼ぶことにします。
㋐を計算すると、 15 17 となり、これは約分の結果です。
(1) 91937 269047 に対して<手順>を行ったとき
①最後の分数を求めてください。
②最後から二番目の分数を求めてください。
(2) 91937 269047 を約分するといくつになりますか。
解答が表示されます













