VOL.123【速さの本質に迫る】 -まとめ-
先日、大学生でも「割合」の意味を正しく理解していない人がいるというような記事を読みました。
数年前にも「平均」の意味が分かっていない人がいるという記事を読んだ記憶があります。
中学受験に向けて勉強している皆さんは「割合」や「平均」の意味は当然分かっているでしょうから、その部分では大学生より上ですね。
こういったことを最近の大学生の学力の低下に結び付けている人もいるようです。
私は今現在、大学教育の現場にいるわけではないので、本当に学力の低下があるかどうかはわかりませんが、私が大学生の頃も勉強ができない人は相当数いたように思います。
例えば、仲間内で問題を出し合うことが流行ったとき「四国4県を全部言え」というのがあったのですが、この問題は少なくとも4人に1人はできなかったと記憶しています。
そして、次の問題の正解率は、ほぼ0%でした。
<例題>
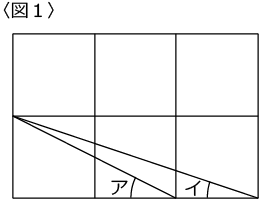
〈図1〉の「 ア + イ 」の角度は何度ですか。
(答)45度
<解説>
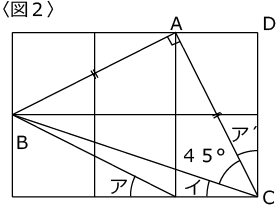
〈図2〉のように補助線をひくと、△ABCは直角三角形になります。
∠ACDはアと等しいので、
90-45=45(度) …(答)
この問題は中学受験では常識とも言えるものですが、私が学生時代は医学部の学生すら即答はできませんでした。
今の受験は、こういった普通に解こうとするとまず解けないような問題を、常識レベルにすることを前提に、さらに思考力に磨きをかけなければいけないという、とんでもなく厳しいものなのです。
そして、このような厳しい状況を経験した今の学生の学力が、昔に比べて低いとはとても思えないのですが・・・
幸いなことに、私が担当した生徒は中学・高校と「数学」の成績が良好なことが多いです。
普段の指導で心がけていることは「受験で結果をだせる」ということが第一ですが、「数学」に「つなげる」ことも多少意識しています。
大学生の学力の向上に少しでも役にたてればうれしいですね。
さて、「速さの本質に迫る」シリーズも今回で最終です。
例によってまとめたいと思います。
このシリーズで特に言いたかったことは2つです。
①最初の方針を誤らない
②比を利用する
①については主にVOL.117で、②についてはVOL.118で述べました。
ここは非常に大切なので、できればもう一度読んでいただければと思います。
今回は上の2つの練習法の具体例を書きたいと思います。
【①の練習法】
私の授業は、問題を編集したプリントを使うことが多いです。
「速さ」の最初の方針を誤らないようにする練習をするときは、シンプルだが少し捻ってある問題を使います。
なぜかというと、基本問題であるならば最初の方針はほぼ決まっていますから、できて当たり前です。
かといって設定が複雑過ぎると、かけた時間に対する見返りが小さくなってしまうので、やはり得策ではありません。
シンプルかどうかの基準は、問題文のボリュームが3~4行程度に収まっていれば、大抵大丈夫です。
少し捻ってあるかどうかはその問題を解いて確認するしかないのですが、問題集や過去問を使う場合はある程度難易度が分かっていると思うので、現在の実力よりも少し上のレベルのものを選べば良いと思います。
そして、その生徒の実力に合わせて編集できればさらに効果的になります。
まだ慣れていない段階では同じ図が連続するようにし、慣れてきたらランダムにするのです。
【②の練習法】
①の練習をする際、「時間の線分図」や「速さの線分図」を描く場合、ほぼ必然的に「比」を使うことになるでしょう。ですから①と②の練習は一緒にすることができます。
また、「グラフ」を描く場合も「比」を意識するように指導しています。
特に「差」をとる場合はそれを「比」にすると良いことが多いです。
また、なかなか「比」を使うことができない場合は「解法縛り」を行います。
具体的には「旅人算禁止」です。
これをやると「比」を使わざるを得ないので、大抵の場合「比」の便利さに気付きます。
どの解法を使うかの選択は本人にかかっているので、本人が心の底から「比」の便利さを実感しないといけません。
「旅人算禁止」がそのきっかけになることでしょう。
「最初の方針を誤らない」「比を利用する」、以上を身に着ければ「速さ」の攻略は手中にしたも同然だと思います。
細かいテーマが少し残っているので、それを書いてまとめとしたいと思います。
| 周回運動 | 池の周りをぐるぐる回るような問題では知識が大切になります。 常識を増やしておきましょう。 |
|---|---|
| 往復の出会い | 1往復なら「線分図」が、何回も往復する場合は「グラフ」がお勧めになります。 「グラフ」は描いてしまえば「図形」ですから、「相似」や「対称性」を利用することができます。 |
| 休憩 | 「休憩」をきちんと表したければ「グラフ」が一番だと思います。 「休憩」がない「グラフ」の一部を平行移動したものをつないだものが「休憩」がある「グラフ」です。これを利用するケースも多いです。 |
| 流水算 | 「速さの線分図」を描くのが基本ですが、それでは対応できない場合は「グラフ」が得策になります。 特に流水の影響を受けないものが出てくる場合など複雑な設定の整理にぴったりです。 |
| 通過算 | 列車の長さがどのような影響を与えるかがわかるような図を描きます。 距離と時間の書き込み方をあらかじめ決めておくと良いでしょう。 |
「速さの本質に迫る」と題し5回にわたり私の考え方を書きました。これを読んでくださった皆さんが「速さ」を得意分野にしてくれるものと期待しています。
具体的な算数の問題に関するご質問など、お子様の中学受験に関してお困りの点がございましたら、こちらのフォームからご質問を承ります。
お寄せいただいたご質問へは当ブログ上にてご回答させていただきます。
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の1題速さ
難易度★★★★☆
池のまわりに1周3600mの一本道があります。
この道を名門君と目白君が自転車と徒歩でそれぞれ1周することにしました。
名門君は時計回り、目白君は反時計回りに同じ地点から同時にスタートしました。
自転車は1台しかなかったので、初めは名門君が自転車に乗りました。
名門君は、ある場所で自転車を降り、その場所に自転車を置いたままにして、徒歩で進みました。
その後、目白君が置いてある自転車に乗って進むと、二人は出発してから16分後に同時にスタート地点に戻ってきました。
次に、二人は同じ方向に進み、できるだけ早く3周することにしました。
こんどは、初めに目白君が自転車に乗り、ある地点に自転車を置くことで、二人は同時にゴールするはずでした。
ところが、目白君が自転車を置いた直後に、いたずら好きの近所の子供が自転車を250m動かしてしまったために、名門君は目白君よりも3分40秒遅れてゴールしました。
目白君は徒歩だと分速75m、自転車に乗ると分速375mで進みます。
名門君は徒歩だと目白君より遅い一定の速さで進み、自転車に乗ると目白君より速い一定の速さで進みます。
(1)名門君の徒歩と自転車に乗ったときの分速はそれぞれ何mですか。
(2)目白君が自転車を置いた地点はスタート地点から何m離れていましたか。
解答が表示されます
(2)1800m













