VOL.82【受験生との歩み】 開成編(2)
前回は成績が良好だったケースでしたが、今回は少し苦しい位置からどうやって合格したのかのお話をしたいと思います。
前田君(仮名)は開成志望でしたが、塾の成績は思ったようには伸びず、15クラス中上から6番目あたりにいました。
本人もこのままではまずいと感じたらしく、個別で習いたいと親に頼んだそうです。
最初は国語を習っていましたが、算数は私が担当するということになりました。ところがスケジュールの関係でなかなか開始することができず、初めての授業は話があってからかなりたっていたと記憶しています。
授業はできていなかったのですが、事前にテストを渡し、それを解いてもらっていたので、学力はある程度把握できていました。
テストの結果と塾の成績から前田君の状態を以下のように診断しました。
- センスに良いものはある。
- 基本知識は身についているが、その運用法や、やや高級な知識に関しては難がある。
- 難問に対して食らいついていく強い気持ちを持っているが、知識の裏付けがないために効率が悪いことが多い。
能力もあり、ある程度きちんと塾の課題もこなしてきたけれど、自分だけでやるにはそろそろ限界、といったところだったと思います。
基本はできていましたから、授業は演習中心に進めました。
それ以外にテスト形式の宿題を出しておき、その直しも授業内でやりました。
このテストは私が過去問からピックアップして作ったもので、中身が濃いものに仕上がったと自負しています。
大体銀本1冊から1、2回分を作ったので、途中から前回購入の話をした関西の学校の過去問を使うなどして、何とか20回分作り上げました。
開成といえば、当時は大問4問で固定されており、全問記述で思考力重視の傾向が続いていました。にもかかわらず、私が出した宿題は答を書くだけの普通のテストでした。
これには理由がありました。
「考える」というのは自分で新しい解法を思いつくというよりも、過去に学んだ解法を目の前の問題に上手くフィットさせることだと思います。
そのためには考え方の基となるエッセンスを身につける必要があります。
そのため、「考え方」がギュッと詰まったテストを宿題に出しました。
単に解法のエッセンスを身につけるだけであるならば、問題はシンプルなほうが良いのです。
そのため、単に答を書くという形式のテストにしました。
そして、それを身につけてもらいながら、授業でその運用法を学ぶというスタイルをとったのです。
一見この方法は誰にでもうまくいきそうなのですが、実はそうでもありません。
宿題をやるのはあくまで生徒自身なので、その取り組み方で大きく差がついてしまうのです。
その点、前田君は素晴らしかったと思います。
何が良かったかというと、まず集中力が凄かったと記憶しています。
名門会の教室には自習室があり、そこで問題を解いている姿を目撃しましたが、小学生であるにもかかわらず、何か迫力のようなものを感じてしまいました。
それと、点数に対するこだわりが強かったのも良かったです。
不本意な点数を取った時は心の底から悔しそうにしていました。
それだけ真剣に宿題をやってくれれば、授業の内容も濃いものになります。
宿題で出てきた内容は共通の認識のようになりますから、レベルの高い話をしてもすんなり理解できることが増えました。
そうこうしているうちにはっきりとした変化が現れました。
Vol.80で取り上げたような問題(数値が煩わしかったり、設定が複雑だったりする問題)でほとんど間違えなくなったのです。
これは、解き方がわかりさえすれば全て正解できることを意味します。
そうなると、私がやるべきことは、解法の幅を広げることになります。
そこで、頻出分野で、知っていると有利になりそうなものを徹底的にやることにしました。
「立体の切断」「グラフを利用する速さ」「整数問題」といった分野のかなり難易度の高いものを授業で取り上げ、根本にある考え方や、記述の仕方といった細かいところまで指導しました。
十分な手ごたえがあったので、ある時、まだやっていなかった過去問を目の前で解いてもらうことにしました。
少し易しめの年度ではあったのですが、前田君は満点を取りました。
この時、はっきりと合格ラインを越えたと確信しました。
結果は予想通り全勝でした。
当時はあの位置(塾で15クラス中6番目あたり)からの合格というのはなかなかないことだったので、私にとっても自信につながるものでした。
いまだにあの時の前田君の集中力を超える生徒には出会っていません。
授業中も、空間の密度が上がったような不思議な感覚を味わいました。
本当に素晴らしかったです。
今は、あの時の感覚を再現できるよう日々の授業を頑張っています。
具体的な算数の問題に関するご質問など、お子様の中学受験に関してお困りの点がございましたら、こちらのフォームからご質問を承ります。
お寄せいただいたご質問へは当ブログ上にてご回答させていただきます。
中学受験・算数の問題などに関する疑問、お困りごとや
金田先生に聞いてみたいことなど、なんでもお気軽におたずねください。
今週の1題規則性
難易度★★★★☆

〈図1〉のように、1から連続した整数が書かれたカードを5枚以上並べ、
次の【規則1】~【規則3】に従って並べかえます。
【規則1】
①1から1つおきにとって並べる。
②残りのカードを①で並べたカードの後に並べる。
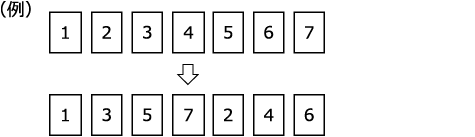
【規則2】
①並べてある枚数を2で割って商を求める。(余りは無視)
②①で求めた商の枚数だけ後ろからとって並べる。
③残りのカードを②で並べたカードの後に並べる。
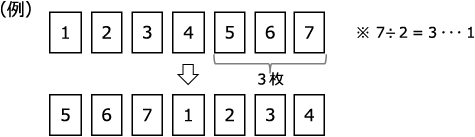
【規則3】
①並べてある枚数を3で割って商を求める。(余りは無視)
②①で求めた商の枚数だけ後ろからとって並べる。
③残りのカードを②で並べたカードの後に並べる。

〈図2〉は5枚のカードに対して【規則1】の操作を4回行い、もとにもどった様子です。
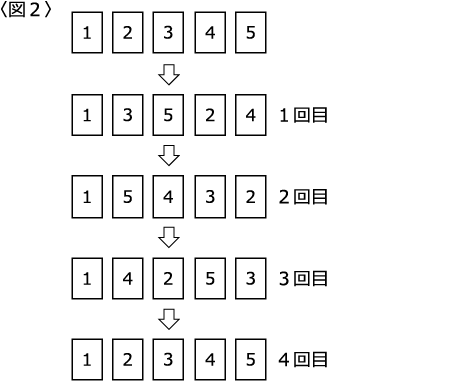
次の(あ)~(お)に適する数字を入れてください。
カードをN枚並べ、まず【規則1】の操作をP回行い、続いて、
【規則2】→【規則1】→【規則3】→【規則1】
の順番で1回ずつ操作を行った。
このとき、1のカードが1番左側に来るようなNとして考えられるものは (あ) 通りある。
また、最初の並び方にもどるようなNとして考えられるものは、
N = (い) … ① 、N = (う) … ② ※(い)<(う)
があり、Pの最小値は、①のときは (え) 、②のときは (お) である。
解答が表示されます













